
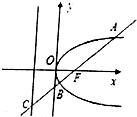
 如图,已知抛物线y2=4x的焦点为F,过F的直线AB交抛物线于A、B,交抛物线的准线于点C,若$\frac{{|{BF}|}}{{|{BC}|}}$=$\frac{1}{2}$,则|AB|=$\frac{16}{3}$.
如图,已知抛物线y2=4x的焦点为F,过F的直线AB交抛物线于A、B,交抛物线的准线于点C,若$\frac{{|{BF}|}}{{|{BC}|}}$=$\frac{1}{2}$,则|AB|=$\frac{16}{3}$. 分析 由题意画出图形,由$\frac{{|{BF}|}}{{|{BC}|}}=\frac{1}{2}$,及抛物线定义求得$∠CBD=\frac{π}{3}$,进一步求得BF,作AE垂直于准线交准线于E点,设|AF|=m,则$|{AE}|=m,\frac{{|{AE}|}}{{|{AC}|}}=\frac{1}{2}$,故$\frac{m}{4+m}=\frac{1}{2}$,求得m值,则AB可求.
解答 解:如图,作BD垂直于准线交准线于D点,
由$\frac{{|{BF}|}}{{|{BC}|}}=\frac{1}{2}$,及抛物线定义可得$cos∠CBD=\frac{{|{BD}|}}{{|{BC}|}}=\frac{1}{2},∠CBD=\frac{π}{3}$,
∴$|{CF}|=4,|{BF}|=\frac{4}{3}$,
作AE垂直于准线交准线于E点,设|AF|=m,则$|{AE}|=m,\frac{{|{AE}|}}{{|{AC}|}}=\frac{1}{2}$,
故$\frac{m}{4+m}=\frac{1}{2}$,解得m=4,
∴|AB|=|AF|+|BF|=4+$\frac{4}{3}=\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题考查抛物线的简单性质,关键是对抛物线定义的熟练应用,是中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<c<a | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用智能手机 | 不使用智能手机 | 合计 | |
| 学习成绩优秀 | 4 | 8 | 12 |
| 学习成绩不优秀 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为使用智能手机对学习有影响 | |
| B. | 有99.5%的把握认为使用智能手机对学习无影响 | |
| C. | 有99.9%的把握认为使用智能手机对学习有影响 | |
| D. | 有99.9%的把握认为使用智能手机对学习无影响 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com