
分析 (1)求出原函数的导函数,得到f′(1),并求得f(1),由直线方程的点斜式得答案;
(2)把不等式f(x)≤0恒成立转化为ax≤-lnx-1,分离参数a得,a≤$\frac{-lnx-1}{x}$.令h(x)=$\frac{-lnx-1}{x}$,利用导数求其最小值得答案;
(3)由(2)知,当a=-1时,lnx-x+1≤0恒成立,即lnx≤x-1,把b1,b2,…,bn放大,再结合错位相减法即可证得Tn<4-$\frac{n+2}{{{2^{n-1}}}}$.
解答 解:(1)∵x>0,f′(x)=$\frac{1}{x}+a$,∴f′(1)=a+1,切点是(1,a+1),
∴f(x)在x=1处的切线方程为y-(a+1)=(a+1)(x-1),即y=(a+1)x;
(2)∵x>0,∴不等式f(x)≤0恒成立,等价于ax≤-lnx-1,即a≤$\frac{-lnx-1}{x}$.
令h(x)=$\frac{-lnx-1}{x}$,则h′(x)=$-\frac{1-lnx}{{x}^{2}}+\frac{1}{{x}^{2}}=\frac{lnx}{{x}^{2}}$.
由h′(x)=0,得x=1.
当x∈(0,1)时,h′(x)<0,h(x)单调递减,
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.
∴h(x)min=h(1)=-1,则a≤-1;
(3)证明:由(2)知,当a=-1时,lnx-x+1≤0恒成立,即lnx≤x-1,当且仅当x=1时取等号.
∴b1=1×ln[($\frac{1}{2}$)1-1+1]<1×[($\frac{1}{2}$)1-1+1-1],
b2=2×ln[($\frac{1}{2}$)2-1+1]<2×[($\frac{1}{2}$)2-1+1-1],
…
bn=n×ln[($\frac{1}{2}$)n-1+1]<n×[($\frac{1}{2}$)n-1+1-1],
∴Tn<1×[($\frac{1}{2}$)1-1+1-1]+2×[($\frac{1}{2}$)2-1+1-1]+…+n×[($\frac{1}{2}$)n-1+1-1]
=1×($\frac{1}{2}$)1-1+2×($\frac{1}{2}$)2-1+…+n×($\frac{1}{2}$)n-1 .
令Sn=1×($\frac{1}{2}$)0+2×($\frac{1}{2}$)1+…+n×($\frac{1}{2}$)n-1 .①
则$\frac{1}{2}$Sn=1×($\frac{1}{2}$)1+2×($\frac{1}{2}$)2+…+n×($\frac{1}{2}$)n .②
①-②得:$\frac{1}{2}{S}_{n}$=$(\frac{1}{2})^{0}+(\frac{1}{2})^{1}+(\frac{1}{2})^{2}+…+(\frac{1}{2})^{n-1}-n(\frac{1}{2})^{n}$=$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}-n•(\frac{1}{2})^{n}$=2-$(n+2)•(\frac{1}{2})^{n}$.
∴${S}_{n}=4-(n+2)•(\frac{1}{2})^{n-1}=4-\frac{n+2}{{2}^{n-1}}$.
∴Tn<4-$\frac{n+2}{{{2^{n-1}}}}$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,训练了错位相减法求数列的和,是压轴题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | ∅=M∩N | B. | ∅⊆M∪N | C. | ∅∈M∩N | D. | ∅∈{M∩N} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline z$=$\frac{1}{2}$-$\frac{1}{2}$i | B. | $\overline z$=-$\frac{1}{2}$-$\frac{1}{2}$i | C. | $\overline z$=-1-i | D. | $\overline z$=1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
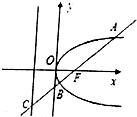 如图,已知抛物线y2=4x的焦点为F,过F的直线AB交抛物线于A、B,交抛物线的准线于点C,若$\frac{{|{BF}|}}{{|{BC}|}}$=$\frac{1}{2}$,则|AB|=$\frac{16}{3}$.
如图,已知抛物线y2=4x的焦点为F,过F的直线AB交抛物线于A、B,交抛物线的准线于点C,若$\frac{{|{BF}|}}{{|{BC}|}}$=$\frac{1}{2}$,则|AB|=$\frac{16}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com