
分析 (Ⅰ)求出函数的导数,得到函数的单调性,求出f(1)f(e)<0,证出结论即可;
(Ⅱ)问题转化为x+$\frac{1+a}{x}$-alnx≥0在[1,e]上恒成立,令h(x)=x+$\frac{1+a}{x}$-alnx,x∈[1,e],通过讨论a的范围,结合函数的单调性求出a的具体范围即可.
解答 解:(Ⅰ)证明:∵f(x)=lnx-$\frac{1}{x}$,x∈[1,e],
则f′(x)=$\frac{1}{x}$+$\frac{1}{{x}^{2}}$>0在[1,e]恒成立,
则f(x)在[1,e]递增,
又f(1)=-1<0,f(e)=1-$\frac{1}{e}$>0,即f(1)•f(e)<0,
∴函数f(x)在[1,e]上存在唯一的零点;
(Ⅱ)由g(x)≥af(x)在[1,e]上恒成立,
则x+$\frac{1}{x}$≥a(lnx-$\frac{1}{x}$),即x+$\frac{1+a}{x}$-alnx≥0在[1,e]上恒成立,
令h(x)=x+$\frac{1+a}{x}$-alnx,x∈[1,e],
则h′(x)=$\frac{(x+1)(x-a-1)}{{x}^{2}}$,
∵x∈[1,e],∴x+1>0,
①1+a≥e即a≥e-1时,h′(x)≤0,h(x)在[1,e]递减,
h(x)min=h(e)=e+$\frac{1+a}{e}$-a,由h(x)min≥0,得:a≤$\frac{{e}^{2}+1}{e-1}$,
即e-1≤a≤$\frac{{e}^{2}+1}{e-1}$;
②1+a≤1即a≤0时,h′(x)≥0,h(x)在[1,e]递增,
h(x)min=h(1)=2+a≥0,解得:a≥-2,
此时:-2≤a≤0;
③1<1+a<e,即0<a<e-1时,
在[1,a+1)上,h′(x)<0,h(x)递减,
在(a+1,e]上,h′(x)>0,h(x)递增,
∴h(x)min=h(a+1)=a+2-aln(a+1),
∵1<1+a<e,∴0<ln(a+1)<1,
∴a+2-aln(1+a)>a+2-a=2>0,
即h(x)min>0恒成立,
∴0<a<e-1符合题意,
综上,a的取值范围是[-2,$\frac{{e}^{2}+1}{e-1}$].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
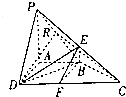 如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,BA⊥AD,AD=CD=2AB,AB∥CD,E,F分别是PC,CD的中点,R是PB上一个动点.
如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,BA⊥AD,AD=CD=2AB,AB∥CD,E,F分别是PC,CD的中点,R是PB上一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用智能手机 | 不使用智能手机 | 合计 | |
| 学习成绩优秀 | 4 | 8 | 12 |
| 学习成绩不优秀 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为使用智能手机对学习有影响 | |
| B. | 有99.5%的把握认为使用智能手机对学习无影响 | |
| C. | 有99.9%的把握认为使用智能手机对学习有影响 | |
| D. | 有99.9%的把握认为使用智能手机对学习无影响 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com