
分析 (1)不等式f(x)≤0,即|2x-a|≤-5x,由x≤-1,可得5x≤2x-a≤-5x,a>0,解出即可得出.
(2)不等式f(x)≥4x+1化为:|2x-a|≥1-x,由不等式f(x)≥4x+1对x∈R恒成立,即|2x-a|≥1-x,对于任意实数成立,可得$1≤\frac{a}{2}$,解出即可得出.
解答 解:(1)不等式f(x)≤0,即|2x-a|≤-5x,∵x≤-1,∴5x≤2x-a≤-5x,a>0,
解得x$≤\frac{a}{7}$,且x≤$-\frac{a}{3}$,∴$-\frac{a}{3}$=-1,解得a=3.
(2)不等式f(x)≥4x+1化为:|2x-a|≥1-x,
∵不等式f(x)≥4x+1对x∈R恒成立,
∴|2x-a|≥1-x,对于任意实数成立,∴$1≤\frac{a}{2}$,解得a≥2.
∴实数a的取值范围是[2,+∞).
点评 本题考查了绝对值不等式的解法、恒成立问题的等价转化方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人 数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
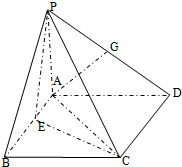 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$(x+1) | B. | y=log2$\sqrt{{x}^{2}-1}$ | ||
| C. | y=log3$\frac{1}{x}$ | D. | y=log${\;}_{\frac{1}{3}}$(x2-4x+3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
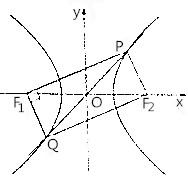 如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )
如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )| A. | 2+$\sqrt{2}$ | B. | 2+$\sqrt{6}$ | C. | $\sqrt{2+\sqrt{2}}$ | D. | $\sqrt{2+\sqrt{6}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com