
分析 (Ⅰ)求导数,利用曲线y=f(x)在(2,f(2))处切线的斜率为$\frac{e^2}{4}$,解出即可;
(Ⅱ)令函数$g(x)=\frac{e^x}{x}$,${g^'}(x)=\frac{{{e^x}(x-1)}}{x^2}$,设函数$h(x)=\frac{{8ln\frac{x}{2}}}{x^2}-x$,${h^'}(x)=\frac{{8-16ln\frac{x}{2}-{x^3}}}{x^3}$,令$φ(x)=8-16ln\frac{x}{2}-{x^3}$,${φ^'}(x)=-\frac{16}{x}-3{x^2}<0$,证明$f(x)=\frac{e^x}{x}-\frac{{8ln\frac{x}{2}}}{x^2}+x\;>g{(x)_{min}}-h{(x)_{max}}=e+2$.
解答 (Ⅰ)解:因为$f(x)=\frac{e^x}{x}-\frac{{aln\frac{x}{2}}}{x^2}+x$,
所以${f^'}(x)=\frac{{{e^x}(x-1)}}{x^2}-\frac{{a-2aln\frac{x}{2}}}{x^3}+1$,…(2分)
则${f^'}(2)=\frac{e^2}{4}-\frac{a}{8}+1=\frac{e^2}{4}$,得a=8.…(4分)
(Ⅱ)证明:$f(x)=\frac{e^x}{x}-\frac{{8ln\frac{x}{2}}}{x^2}+x$,x∈(0,+∞),
设函数$g(x)=\frac{e^x}{x}$,${g^'}(x)=\frac{{{e^x}(x-1)}}{x^2}$,…(6分)
当x∈(0,1)时,g′(x)<0,g(x)为减函数,
当x∈(1,+∞)时,g′(x)>0,g(x)为增函数,
则g(x)≥g(1)=e.…(8分)
设函数$h(x)=\frac{{8ln\frac{x}{2}}}{x^2}-x$,${h^'}(x)=\frac{{8-16ln\frac{x}{2}-{x^3}}}{x^3}$,
令$φ(x)=8-16ln\frac{x}{2}-{x^3}$,${φ^'}(x)=-\frac{16}{x}-3{x^2}<0$,
则$φ(x)=8-16ln\frac{x}{2}-{x^3}$在x∈(0,+∞)为减函数,…(10分)
又因为φ(2)=0,则当x∈(0,2)时,φ(x)>0,即h′(x)>0,h(x)为增函数,
则当x∈(2,+∞)时,φ(x)<0,即h′(x)<0,h(x)为减函数,
所以h(x)≤h(2)=-2,
综上所述,$f(x)=\frac{e^x}{x}-\frac{{8ln\frac{x}{2}}}{x^2}+x\;>g{(x)_{min}}-h{(x)_{max}}=e+2$.…(12分)
点评 本题考查利用导数研究曲线上某点切线方程及函数的最值问题,(Ⅱ)问关键是构造函数,转化为求函数的最值解决.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 4m | 3 |
| y | m | 3 | 5.5 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
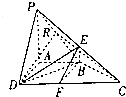 如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,BA⊥AD,AD=CD=2AB,AB∥CD,E,F分别是PC,CD的中点,R是PB上一个动点.
如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,BA⊥AD,AD=CD=2AB,AB∥CD,E,F分别是PC,CD的中点,R是PB上一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com