
| A. | y=log${\;}_{\frac{1}{2}}$(x+1) | B. | y=log2$\sqrt{{x}^{2}-1}$ | ||
| C. | y=log3$\frac{1}{x}$ | D. | y=log${\;}_{\frac{1}{3}}$(x2-4x+3) |
分析 根据对数函数与其他基本初等函数的复合函数单调性,对选项中的函数单调性进行判断即可.
解答 解:对于A,函数y=${log}_{\frac{1}{2}}$(x+1)的定义域是(-1,+∞),且在(0,1)上为减函数,不满足题意;
对于B,函数y=log2$\sqrt{{x}^{2}-1}$的定义域是(-∞,-1)∪(1,+∞),所以在(0,1)上无意义,不满足题意;
对于C,函数y=log3$\frac{1}{x}$的定义域是(-∞,0)∪(0,+∞),且在(0,1)上为减函数,不满足题意;
对于D,函数y=${log}_{\frac{1}{3}}$(x2-4x+3)的定义域是(-∞,1)∪(1,+∞),且在(0,1)上为增函数,满足题意.
故选:D.
点评 本题考查了对数函数与其他基本初等函数的复合函数单调性判断问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
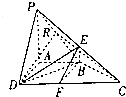 如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,BA⊥AD,AD=CD=2AB,AB∥CD,E,F分别是PC,CD的中点,R是PB上一个动点.
如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,BA⊥AD,AD=CD=2AB,AB∥CD,E,F分别是PC,CD的中点,R是PB上一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
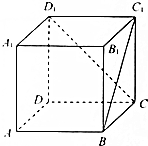 如图,ABCD-A1B1C1D1是棱长为a的正方体;
如图,ABCD-A1B1C1D1是棱长为a的正方体;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com