
分析 (1)求出函数的导数,求出切点坐标,切线斜率,即可得到所求切线方程.
(2)通过$f(x)>2g(x)⇒3{a^2}-a<\frac{x^2}{2lnx}$,对?x>1恒成立;构造函数$h(x)=\frac{x^2}{2lnx}$,求出导数求出极值点,判断函数的单调性,求解函数的最值,即可推出a的范围.
解答 解:(1)依题意,$f(x)={x^2}-4lnx,f'(x)=2x-\frac{4}{x}$,
故f'(1)=-2,因为f(1)=1,…(3分)
故所求切线方程为y-1=-2(x-1),得y=-2x+3;…(4分)
(2)依题意,因为x∈(1,+∞),故lnx>0,
故$f(x)>2g(x)⇒3{a^2}-a<\frac{x^2}{2lnx}$,对?x>1恒成立;…(6分)
令$h(x)=\frac{x^2}{2lnx}$,则$h'(x)=\frac{{x({2lnx-1})}}{{2{{({lnx})}^2}}}$,令h'(x)=0,得$x=\sqrt{e}$,
当$x∈({1,\sqrt{e}})$时,h(x)单调递减;$x∈({\sqrt{e},+∞})$时,h(x)单调递增…(8分)
所以当$x=\sqrt{e}$时,h(x)取得最小值$h({\sqrt{e}})=e$…(9分)
∴$3{a^2}-a<e⇒\frac{{1-\sqrt{1+12e}}}{6}<a<\frac{{1+\sqrt{1+12e}}}{6}$…(11分)
又∵$a≤\frac{1}{2}$,∴$\frac{{1-\sqrt{1+12e}}}{6}<a≤\frac{1}{2}$…(12分)
点评 本题考查函数的导数的综合应用,切线方程以及函数的单调性,函数的最值,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人 数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$(x+1) | B. | y=log2$\sqrt{{x}^{2}-1}$ | ||
| C. | y=log3$\frac{1}{x}$ | D. | y=log${\;}_{\frac{1}{3}}$(x2-4x+3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
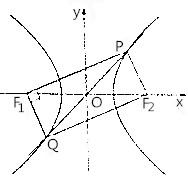 如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )
如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )| A. | 2+$\sqrt{2}$ | B. | 2+$\sqrt{6}$ | C. | $\sqrt{2+\sqrt{2}}$ | D. | $\sqrt{2+\sqrt{6}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月消费金额(单位:元) | [0,100) | [100,200) | [200,300) | [300,400) | [400,500) | ≥500 |
| 人数 | 30 | 6 | 9 | 10 | 3 | 2 |
| 高消费 | 非高消费 | 合计 | |
| 男生 | 10 | 20 | 30 |
| 女生 | 5 | 25 | 30 |
| 合计 | 15 | 45 | 60 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com