
分析 根据绝对值的性质得出-$\frac{1}{100}$<$\frac{3n}{n+1}$-3<$\frac{1}{100}$,再根据不等式的性质求解即可.
解答 解:∵|$\frac{3n}{n+1}$-3|<$\frac{1}{100}$,
∴-$\frac{1}{100}$<$\frac{3n}{n+1}$-3<$\frac{1}{100}$,
∴3-$\frac{1}{100}$<$\frac{3n}{n+1}$<$\frac{1}{100}$+3,
∴n>299,
∴使不等式|$\frac{3n}{n+1}$-3|<$\frac{1}{100}$成立的最小正整数n为300.
点评 本题考查绝对值不等式和分式不等式.解不等式要用到不等式的性质:(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式的两边乘(或除以)同一个负数,不等号的方向改变.


科目:高中数学 来源: 题型:选择题
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | 11.38万元 | B. | 12.38万元 | C. | 13.38万元 | D. | 14.38万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人 数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间 (分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
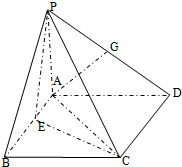 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$(x+1) | B. | y=log2$\sqrt{{x}^{2}-1}$ | ||
| C. | y=log3$\frac{1}{x}$ | D. | y=log${\;}_{\frac{1}{3}}$(x2-4x+3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com