
分析 (1)利用特殊值法判断即可;
(2)根据条件,逐步代入求解;
(3)猜想结论,根据数学归纳法的证明步骤证明.
解答 解:(1)令x=y=0,得f(0+0)=f(0)+f(0)+2×0×0,得f(0)=0.…(2分)
(2)由f(1)=1,得f(2)=f(1+1)=f(1)+f(1)+2×1×1=4.
f(3)=f(2+1)=f(2)+f(1)+2×2×1=9.f(4)=f(3+1)=f(3)+f(1)+2×3×1=16.…(5分)
(3)由(2)可猜想f(n)=n2,…(7分)
用数学归纳法证明:
(i)当n=1时,f(1)=12=1显然成立.…(8分)
(ii)假设当n=k时,命题成立,即f(k)=k2,…(10分)
则当n=k+1时,f(k+1)=f(k)+f(1)+2×k×1=k2+1+2k=(k+1)2,
故当n=k+1时命题也成立,…(12分)
由(i),(ii)可得,对一切n∈N*都有f(n)=n2成立.…(14分)
点评 考查了特殊法解决抽象函数问题和数学归纳法证明的步骤,属于基础题型,应熟练掌握.


科目:高中数学 来源: 题型:解答题
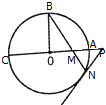 如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 无解 | B. | 恰有一解 | C. | 恰有两个解 | D. | 有无穷多个解 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将△ABE 沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将△ABE 沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<c<a | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com