
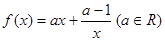 ,
,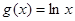 .
.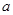 ,函数
,函数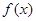 与
与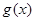 的图象在
的图象在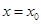 处的切线斜率总相等,求
处的切线斜率总相等,求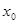 的值;
的值;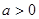 ,对任意
,对任意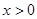 ,不等式
,不等式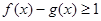 恒成立,求实数
恒成立,求实数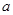 的取值范围.
的取值范围.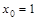 ;(2)
;(2)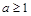 .
.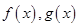 的导数,由题设知
的导数,由题设知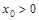 ,且
,且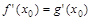 ,解得
,解得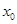 即可;(2)两种方法:法一,先利用在
即可;(2)两种方法:法一,先利用在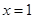 处不等式成立,得
处不等式成立,得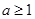 ,即
,即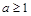 是不等式
是不等式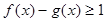 恒成立的必要条件,再说明
恒成立的必要条件,再说明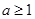 是不等式
是不等式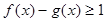 恒成立的充分条件即可;法二,记
恒成立的充分条件即可;法二,记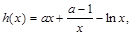 则在
则在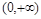 上,
上,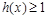 ,对
,对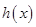 求导,对
求导,对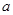 讨论求出满足
讨论求出满足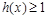 的
的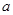 的范围.
的范围.
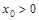 ,且
,且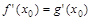 ,即
,即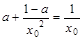 , ……2分
, ……2分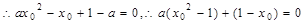
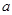 恒成立,
恒成立,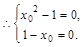 ……4分
……4分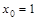 ……5分
……5分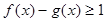 即
即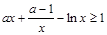 ,
,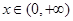 时
时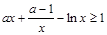 恒成立,则在
恒成立,则在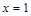 处必成立,即
处必成立,即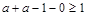 ,
,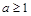 是不等式
是不等式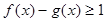 恒成立的必要条件. ……7分
恒成立的必要条件. ……7分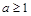 时,记
时,记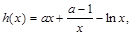 则在
则在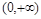 上,
上,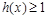
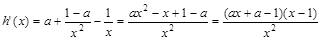 ……9分
……9分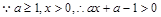
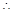
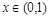 时
时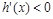 ,
,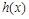 单调递减;
单调递减;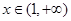 时
时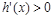 ,
,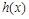 单调递增
单调递增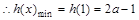
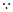
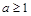 ,
,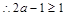 ,即
,即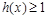 恒成立
恒成立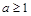 是不等式
是不等式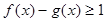 恒成立的充分条件. ……11分
恒成立的充分条件. ……11分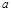 的取值范围是
的取值范围是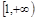 ……12分
……12分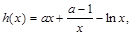 则在
则在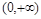 上,
上,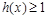
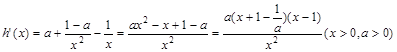 ……7分
……7分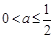 ,
,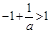 ,
,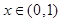 时,
时,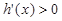 ,
,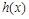 单调递增,
单调递增,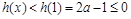 ,
,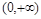 上
上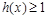 矛盾; ……8分
矛盾; ……8分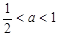 ,
,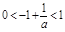 ,
,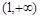 上
上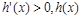 递增,而
递增,而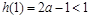 ,
,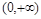 上
上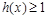 矛盾;……9分
矛盾;……9分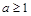 ,
,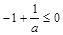 ,
,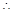
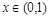 时
时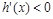 ,
,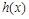 单调递减;
单调递减;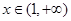 时
时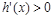 ,
,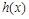 单调递增
单调递增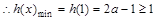 ,即
,即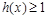 恒成立 11分
恒成立 11分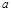 的取值范围是
的取值范围是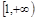 12分
12分

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com