
设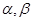 为使互不重合的平面,
为使互不重合的平面,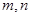 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题:
①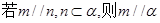
②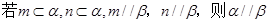
③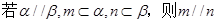
④若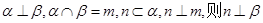 ;
;
其中正确命题的序号为 .
④
解析试题分析:根据线面平行的判定定理,面面平行的判定定理,面面平行的性质定理,及面面垂直的性质定理,对题目中的四个结论逐一进行分析,即可得到答案.
解:当m∥n,n?α,,则m?α也可能成立,故①错误;
当m?α,n?α,m∥β,n∥β,m与n相交时,α∥β,但m与n平行时,α与β不一定平行,故②错误;
若α∥β,m?α,n?β,则m与n可能平行也可能异面,故③错误;
若α⊥β,α∩β=m,n?α,n⊥m,由面面平行的性质,易得n⊥β,故④正确
故答案为:④
考点:本题考查的知识点是平面与平面之间的位置关系,直线与平面之间的位置关系。
点评:熟练掌握空间线与线,线与面,面与面之间的关系的判定方法及性质定理,是解答本题的关键,属于基础题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,则
,则 ;
;
③若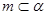 ,
,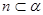 ,
, ,
, ,则
,则 ;
;
④若 ,
, ,
, ,
,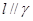 ,则
,则 。
。
其中命题正确的是 .(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com