
如图,直线 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(1)用 、
、 表示出
表示出 点、
点、 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于 轴;
轴;
(2)求 的面积,证明
的面积,证明 的面积与
的面积与 、
、 无关,只与
无关,只与 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连 、
、 ,再作与
,再作与 、
、 平行的切线,切点分别为
平行的切线,切点分别为 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
(1)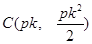 ,
,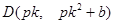 ,(2)
,(2)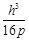 ,(3)能.
,(3)能.
解析试题分析:(1)因为D点为直线与抛物线的交点A,B中点,所以求D点坐标就根据直线方程与抛物线方程联立方程组,利用韦达定理求解,即由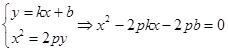 ,得
,得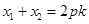 ,
,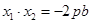 ,点
,点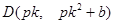 .因为C点为切点,利用切线方程与抛物线方程联立方程组后的判别式为零进行求解,即由
.因为C点为切点,利用切线方程与抛物线方程联立方程组后的判别式为零进行求解,即由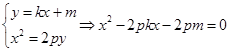 ,得
,得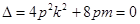 ,得
,得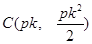 .由于
.由于 、
、 的横坐标相同,
的横坐标相同,
 垂直于
垂直于 轴.(2)求三角形面积,必须观察结构,合理选用底边与高.本题将CD选为底,则
轴.(2)求三角形面积,必须观察结构,合理选用底边与高.本题将CD选为底,则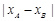 为高,利用(1)求出
为高,利用(1)求出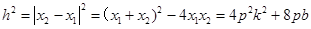 ,则
,则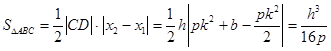 ,(3)对题目“马上”的理解,就是进行类比,直接写出结论. 由(1)知
,(3)对题目“马上”的理解,就是进行类比,直接写出结论. 由(1)知 垂直于
垂直于 轴,
轴,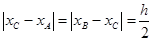 ,由(2)可得
,由(2)可得 、
、 的面积只与
的面积只与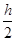 有关,将
有关,将 中的
中的 换成
换成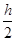 ,可得
,可得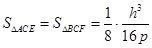 .而这一过程可无限类比下去,依次得到一列数:
.而这一过程可无限类比下去,依次得到一列数: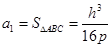 ,
,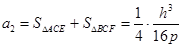 ,这些数构成一个公比为
,这些数构成一个公比为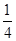 无穷等比数列,其和可看成直线
无穷等比数列,其和可看成直线 与抛物线围成的面积,即
与抛物线围成的面积,即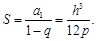
试题解析:(1)由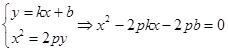 ,得
,得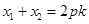 ,
,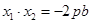
点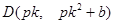 2分
2分
设切线方程为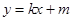 ,由
,由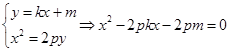 ,得
,得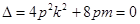 ,
,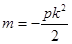 ,切点的横坐标为
,切点的横坐标为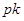 ,得
,得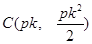 4分
4分
由于 、
、 的横坐标相同,
的横坐标相同,
 垂直于
垂直于 轴. 6分
轴. 6分
(2)
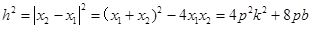 ,
,
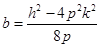 . 8分
. 8分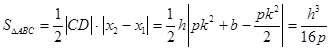 . 11分
. 11分 的面积与
的面积与 、
、 无关,只与
无关,只与 有关. 12分
有关. 12分
(本小题也可以求 ,切点到直线
,切点到直线 的距离
的距离 ,相应给分)
,相应给分)
(3)由(1)知 垂直于
垂直于 轴,
轴,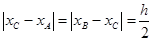 ,由(2)可得
,由(2)可得 、
、 的面积只与
的面积只与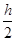 有关,将
有关,将 中的
中的 换成
换成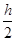 ,可得
,可得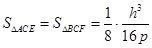 . 14分
. 14分
记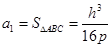 ,
,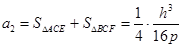


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
已知抛物线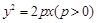 的焦点为
的焦点为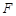 ,点
,点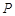 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,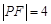 .
.
(1)求抛物线的方程;
(2) 设点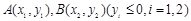 是抛物线上的两点,
是抛物线上的两点,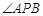 的角平分线与
的角平分线与 轴垂直,求
轴垂直,求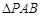 的面积最大时直线
的面积最大时直线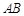 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 的离心率
的离心率 ,且直线
,且直线 是抛物线
是抛物线 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P  为椭圆上一点,直线
为椭圆上一点,直线 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆C上一点与两个焦点F1,F2构成的三角形的周长为2
,且椭圆C上一点与两个焦点F1,F2构成的三角形的周长为2 +2.
+2.
(1)求椭圆C的方程;
(2)过右焦点F2作直线l 与椭圆C交于A,B两点,设 ,若
,若 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4.
(1)求椭圆 的方程;
的方程;
(2)已知直线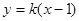 与椭圆
与椭圆 交于
交于 、
、 两点,试问,是否存在
两点,试问,是否存在 轴上的点
轴上的点 ,使得对任意的
,使得对任意的 ,
, 为定值,若存在,求出
为定值,若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 :
: (
( )的右焦点为
)的右焦点为 ,且椭圆
,且椭圆 过点
过点 .
.
(1)求椭圆 的方程;
的方程;
(2)设斜率为 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、 ,以线段
,以线段 为底边作等腰三角形
为底边作等腰三角形 ,其中顶点
,其中顶点 的坐标为
的坐标为 ,求△
,求△ 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图已知抛物线 :
: 过点
过点 ,直线
,直线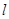 交
交 于
于 ,
, 两点,过点
两点,过点 且平行于
且平行于 轴的直线分别与直线
轴的直线分别与直线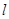 和
和 轴相交于点
轴相交于点 ,
, .
.
(1)求 的值;
的值;
(2)是否存在定点 ,当直线
,当直线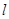 过点
过点 时,△
时,△ 与△
与△ 的面积相等?若存在,求出点
的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆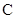 :
: (
(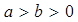 )的右焦点
)的右焦点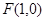 ,右顶点
,右顶点 ,且
,且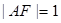 .
.
(1)求椭圆 的标准方程;
的标准方程;
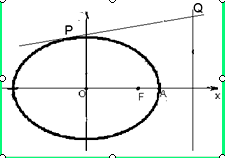
(2)若动直线 :
: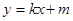 与椭圆
与椭圆 有且只有一个交点
有且只有一个交点 ,且与直线
,且与直线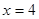 交于点
交于点 ,问:是否存在一个定点
,问:是否存在一个定点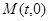 ,使得
,使得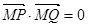 .若存在,求出点
.若存在,求出点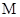 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆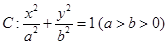 经过点
经过点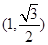 ,离心率为
,离心率为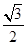 .
.
(1)求椭圆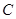 的方程;
的方程;
(2)直线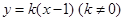 与椭圆
与椭圆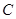 交于
交于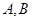 两点,点
两点,点 是椭圆
是椭圆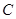 的右顶点.直线
的右顶点.直线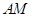 与直线
与直线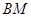 分别与
分别与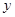 轴交于点
轴交于点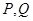 ,试问以线段
,试问以线段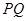 为直径的圆是否过
为直径的圆是否过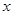 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com