考点:两角和与差的正弦函数,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:计算题,三角函数的图像与性质
分析:(1)根据函数的最大值,可得A=1.算出周期T=4(
-)=2π,可得ω=
=1.再将
(,1)代入得到关于ϕ的等式,结合
<ϕ<解出
ϕ=,即可得出函数y=f(x)的表达式;
(2)由(1)得
f(α)=sin(α+)=,利用同角三角函数的关系算出
cos(α+)=,再进行配角:α=(α+
)-
,根据两角差的正弦公式加以计算,可得sinα的值.
解答:
解:(1)由图象,可得函数的最大值为A=1,
最小正周期T=4(
-)=2π,可得ω=
=1.
由此可得f(x)=sin(x+ϕ),将
(,1)代入,
可得
sin(+ϕ)=1,
∵
-<ϕ<
,可得
-<+ϕ<,
∴
+ϕ=,解得
ϕ=,
因此,函数y=f(x)的表达式是
f(x)=sin(x+),x∈R;
(2)由
f(α)=,得
sin(α+)=,
∵
-<α<,可得
<α+<,
∴
cos(α+)==
.
由此可得:
| | sinα=sin[(α+)-]=sin(α+)cos-cos(α+)sin |
| |
=
.
点评:本题给出三角函数的图象,求函数的解析式,并依此求sinα的值.着重考查了由三角函数的部分图象确定其解析式、同角三角函数的基本关系、两角和与差的三角函数公式等知识,属于中档题.

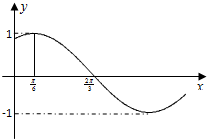 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,-

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案