
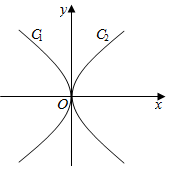
 已知抛物线C1:y2=-4x的准线经过抛物线C2:y2=2px的焦点
已知抛物线C1:y2=-4x的准线经过抛物线C2:y2=2px的焦点分析 (I)求出抛物线C1的准线方程和抛物线C2的焦点,将焦点坐标带诶准线方程得出p,即可得出抛物线的方程;
(II)设M(-$\frac{{{y}_{1}}^{2}}{4}$,y1),N($\frac{{{y}_{2}}^{2}}{4}$,y2),根据$\overrightarrow{OM}$+λ$\overrightarrow{OQ}$=$\overrightarrow{ON}$求出Q的坐标,代入抛物线C2的方程得出λ关于y1,y2的函数,利用基本不等式求出λ的范围.
解答 解:(I)抛物线C1的准线方程为:x=1,
抛物线C2的交点坐标为($\frac{p}{2}$,0),
∴$\frac{p}{2}=1$,解得p=2.
∴抛物线C2的方程为:y2=4x.
(II)设M(-$\frac{{{y}_{1}}^{2}}{4}$,y1),N($\frac{{{y}_{2}}^{2}}{4}$,y2),(y1<0,y2>0).
∵$\overrightarrow{OM}$+λ$\overrightarrow{OQ}$=$\overrightarrow{ON}$,∴$λ\overrightarrow{OQ}$=$\overrightarrow{ON}-\overrightarrow{OM}$=($\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{4}$,y2-y1),
∴Q($\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{4λ}$,$\frac{{y}_{2}-{y}_{1}}{λ}$).
∵Q在抛物线C2:y2=4x上,
∴$\frac{({y}_{2}-{y}_{1})^{2}}{{λ}^{2}}=\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{λ}$,∴λ=$\frac{({y}_{2}-{y}_{1})^{2}}{{{y}_{1}}^{2}+{{y}_{2}}^{2}}$=1-$\frac{2{y}_{1}{y}_{2}}{{{y}_{1}}^{2}+{{y}_{2}}^{2}}$.
∵y12+y22≥-2y1y2>0,
∴0<-$\frac{2{y}_{1}{y}_{2}}{{{y}_{1}}^{2}+{{y}_{2}}^{2}}$≤1.
∴1<λ≤2.
点评 本题考查了抛物线的性质,向量的线性运算,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,0) | C. | (0,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
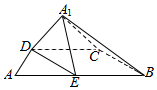 已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.
已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com