
分析 (Ⅰ)先求出函数的表达式,利用导数研究其单调性极值与最值即可得出;
(Ⅱ)当x≥1时,不等式f(x)>$\frac{2sinx}{{x({x+1})}}$,等价于$\frac{(x+1)(1+lnx)}{x}$>2sinx,构造g(x)=$\frac{(x+1)(1+lnx)}{x}$(x≥1),证明g(x)在[1,+∞)上是单调递增,所以[g(x)]min=g(1)=2,即可得出结论.
解答 解:(Ⅰ)由xf′(x)+2f(x)=$\frac{1}{{x}^{2}}$,
变形为(x2f(x))′=(lnx)′,
∴f(x)=$\frac{lnx+C}{{x}^{2}}$,
∵f(1)=1,∴C=1.
∴f(x)=$\frac{lnx+1}{{x}^{2}}$,(x>0),
∴f′(x)=$\frac{-1-2lnx}{{x}^{3}}$,
令f′(x)>0,解得:0<x<$\frac{1}{\sqrt{e}}$,
令f′(x)<0,解得:x>$\frac{1}{\sqrt{e}}$,
∴f(x)在(,$\frac{1}{\sqrt{e}}$)递增,在($\frac{1}{\sqrt{e}}$,+∞)递减,
∴f(x)最大值=f($\frac{1}{\sqrt{e}}$)=$\frac{e}{2}$;
(Ⅱ)证明:当x≥1时,不等式f(x)>$\frac{2sinx}{{x({x+1})}}$,
等价于 $\frac{(x+1)(1+lnx)}{x}$>2sinx.
记g(x)=$\frac{(x+1)(1+lnx)}{x}$(x≥1)
所以g′(x)=$\frac{x-lnx}{{x}^{2}}$,
令h(x)=x-lnx,则h′(x)=1-$\frac{1}{x}$,
由x≥1得h′(x)≥0,所以h(x)在[1,+∞)上单调递增,
所以[h(x)]min=h(1)=1>0,
从而g′(x)>0.
故g(x)在[1,+∞)上是单调递增,所以[g(x)]min=g(1)=2,
因为当x≥1时,2sinx≤2,所以g(x)≥2sinx,
又因为当x=1时,2sinx=2sin1<2,
所以当x≥1时,g(x)>2sinx,即 $\frac{(x+1)(1+lnx)}{x}$>2sinx,
所以当x≥1时,不等式f(x)>$\frac{2sinx}{{x({x+1})}}$恒成立.
点评 本题考查了利用导数研究函数的单调性极值与最值、构造法,考查了变形能力、推理能力与计算能力,属于难题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 24种 | C. | 48种 | D. | 120种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(2,+∞) | D. | (0,2)∪(-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1$<x<\sqrt{2}$} | B. | {x|x>1或x<-1} | C. | {x|-1<x<1} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知F为抛物线y2=2x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F.
如图,已知F为抛物线y2=2x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
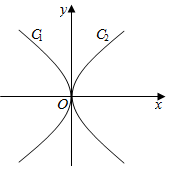 已知抛物线C1:y2=-4x的准线经过抛物线C2:y2=2px的焦点
已知抛物线C1:y2=-4x的准线经过抛物线C2:y2=2px的焦点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com