
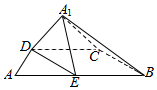
 已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.
已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.分析 (I)过A1作A1H⊥CD交CD于H,连结CE,则可证四边形ADCE是矩形,得出CE⊥CD,由A1H⊥平面BCDE得出A1H⊥CE,于是CE⊥平面A1DC,故而平面A1EC⊥平面A1DC;
(II)利用勾股定理计算A1H,BH,A1B,于是直线A1B与平面EBCD所成角的正弦值为$\frac{{A}_{1}H}{{A}_{1}B}$.
解答 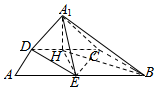 证明:(I)过A1作A1H⊥CD交CD于H,连结CE.
证明:(I)过A1作A1H⊥CD交CD于H,连结CE.
∵点A1在平面EBCD上的射影H在直线CD上,
∴A1H⊥平面EBCD.∵CE?平面EBCD,
∴A1H⊥CE.
∵AB∥CD,∠A=$\frac{π}{2}$,CD=AE=$\frac{1}{2}AB$,
∴四边形AECD是矩形,∴CE⊥CD.
又A1H?平面A1DC,CD?平面A1DC,A1H∩CD=H,
∴CE⊥平面A1DC,
∵CE?平面A1CE,
平面A1EC⊥平面A1DC.
解:(II)连结BH,∵A1H⊥平面EBCD,∴∠A1BH为直线A1B与平面EBCD所成的角.
连结HE,设A1H=x,则DH=$\sqrt{1-{x}^{2}}$,HE=$\sqrt{4-{x}^{2}}$,
∴CH=$\sqrt{H{E}^{2}-C{E}^{2}}$=$\sqrt{3-{x}^{2}}$.
∴$\sqrt{1-{x}^{2}}$+$\sqrt{3-{x}^{2}}$=2,解得x=$\frac{\sqrt{3}}{2}$,
∴A1H=$\frac{\sqrt{3}}{2}$,DH=$\frac{1}{2}$,
∴BH=$\sqrt{(4-\frac{1}{2})^{2}+{1}^{2}}$=$\frac{\sqrt{53}}{2}$,
∴A1B=$\sqrt{{A}_{1}{H}^{2}+B{H}^{2}}$=$\sqrt{14}$.
∴sin∠A1BH=$\frac{{A}_{1}H}{{A}_{1}B}$=$\frac{\sqrt{42}}{28}$.
∴直线A1B与平面EBCD所成角的正弦值为$\frac{\sqrt{42}}{28}$.
点评 本题考查了面面垂直的判定,线面角的计算,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
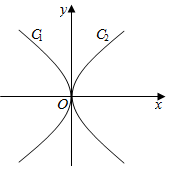 已知抛物线C1:y2=-4x的准线经过抛物线C2:y2=2px的焦点
已知抛物线C1:y2=-4x的准线经过抛物线C2:y2=2px的焦点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-2=0 | B. | x+y-2=0 | C. | x±y-2=0 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com