
分析 可作出图形,根据题意可知λ,μ>0,根据条件对$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$两边平方,进行数量积的运算化简,利用三角代换以及两角和与差的三角函数,从而便可得出2λ+$\sqrt{3}$μ的最大值.
解答 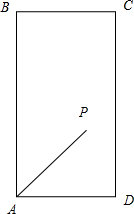 解:如图,依题意知,λ>0,μ>0;
解:如图,依题意知,λ>0,μ>0;
根据条件,
1=$\overrightarrow{AP}$2=λ2$\overrightarrow{AB}$2+2λμ$\overrightarrow{AB}$•$\overrightarrow{AD}$+μ2$\overrightarrow{AD}$2
=4λ2+μ2.令λ=$\frac{1}{2}cosθ$,μ=sinθ.
∴2λ+$\sqrt{3}$μ=cosθ+$\sqrt{3}$sinθ=2sin(θ+$\frac{π}{6}$)≤2;
∴2λ+$\sqrt{3}$μ的最大值为:2.此时θ=$\frac{π}{3}$
故答案为:$\frac{π}{3}$.
点评 考查向量数量积的运算及计算公式,以及配方法的应用,三角代换的应用,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
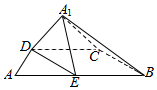 已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.
已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
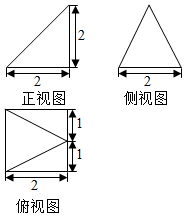 已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为$\frac{8}{3}$,表面积为$6+2\sqrt{5}+2\sqrt{2}$.
已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为$\frac{8}{3}$,表面积为$6+2\sqrt{5}+2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$) | B. | (-∞,$\frac{9}{4}$) | C. | (-$\frac{3}{2}$,$\frac{9}{4}$) | D. | ($\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com