
分析 (Ⅰ)利用抛物线的定义,结合抛物线C:y2=2px(p>0)过点M(m,2),且|MF|=2,求出p,即可求抛物线C的方程;
(Ⅱ)设EA:y=kx+t联立$\left\{\begin{array}{l}y=kx+t\\{y^2}=4x\end{array}\right.$,消去y,可得k2x2+(2kt-4)x+t2=0,利用直线EA与抛物线C相切,得到kt=1代入$\frac{1}{t^2}{x^2}-2x+{t^2}=0$,求出A的坐标;由几何性质可以判断点O,B关于直线EF:y=-tx+t对称,求出B的坐标,证明kAF=kBF,即A,B,F三点共线;当t=±1时,A(1,±2),B(1,±1),此时A,B,F共线.
解答 (I)解:抛物线C的准线方程为:$x=-\frac{p}{2}$,
∴$|MF|=m+\frac{p}{2}=2$,
又抛物线C:y2=2px(p>0)过点M(m,2),
∴4=2pm,即$4=2p(2-\frac{p}{2})$…(2分)
∴p2-4p+4=0,∴p=2,
∴抛物线C的方程为y2=4x.…(4分)
(II)证明;设E(0,t)(t≠0),已知切线不为y轴,设EA:y=kx+t联立$\left\{\begin{array}{l}y=kx+t\\{y^2}=4x\end{array}\right.$,消去y,可得k2x2+(2kt-4)x+t2=0
∵直线EA与抛物线C相切,∴△=(2kt-4)2-4k2t2=0,即kt=1.
代入$\frac{1}{t^2}{x^2}-2x+{t^2}=0$,∴x=t2,即A(t2,2t),…(6分)
设切点B(x0,y0),则由几何性质可以判断点O,B关于直线EF:y=-tx+t对称,
则$\left\{\begin{array}{l}\frac{y_0}{x_0}×\frac{t-0}{0-1}=-1\\ \frac{y_0}{2}=-t•\frac{x_0}{2}+t\end{array}\right.$,解得:$\left\{\begin{array}{l}{x_0}=\frac{{2{t^2}}}{{{t^2}+1}}\\{y_0}=\frac{2t}{{{t^2}+1}}\end{array}\right.$,即$B(\frac{{2{t^2}}}{{{t^2}+1}},\frac{2t}{{{t^2}+1}})$…(8分)
直线AF的斜率为${k_{AF}}=\frac{2t}{{{t^2}-1}}(t≠±1)$,
直线BF的斜率为${k_{BF}}=\frac{{\frac{2t}{{{t^2}+1}}-0}}{{\frac{{2{t^2}}}{{{t^2}+1}}-1}}=\frac{2t}{{{t^2}-1}}(t≠±1)$,∴kAF=kBF,即A,B,F三点共线.…(10分)
当t=±1时,A(1,±2),B(1,±1),此时A,B,F共线.
综上:A,B,F三点共线.…(12分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查直线斜率的计算,考查学生分析解决问题的能力,计算量大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
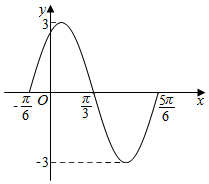 如图是函数$f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<\frac{π}{2})$的图象的一部分.
如图是函数$f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<\frac{π}{2})$的图象的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,0) | C. | (0,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
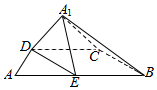 已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.
已知直角梯形ABCD中,AB∥CD,∠A=$\frac{π}{2}$,AD=1,AB=2CD=4,E为AB中点,沿线段DE将△ADE折起到△A1DE,使得点A1在平面EBCD上的射影H在直线CD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>2 | B. | 0<k<2 | C. | 0<k<4 | D. | k>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
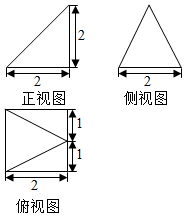 已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为$\frac{8}{3}$,表面积为$6+2\sqrt{5}+2\sqrt{2}$.
已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为$\frac{8}{3}$,表面积为$6+2\sqrt{5}+2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com