
| A. | k>2 | B. | 0<k<2 | C. | 0<k<4 | D. | k>0 |
分析 由k>0,可得椭圆$\frac{{x}^{2}}{k}$+$\frac{{y}^{2}}{k+2}$=1的焦点在y轴上,求得焦点和短轴的端点坐标,运用点在圆内转化为点与圆心的距离小于半径,解不等式即可得到所求范围.
解答 解:由k>0,可得椭圆$\frac{{x}^{2}}{k}$+$\frac{{y}^{2}}{k+2}$=1的焦点在y轴上,
即有焦点为F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),
短轴的端点为A(-$\sqrt{k}$,0),B($\sqrt{k}$,0),
由短轴端点在以椭圆两焦点连线段为直径的圆内,
可得|OA|<|OF1|,即有$\sqrt{k}$<$\sqrt{2}$,
解得0<k<2.
故选:B.
点评 本题考查椭圆的方程和性质,注意运用转化思想,将点在圆内转化为点与圆心的距离小于半径,考查运算能力,属于基础题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
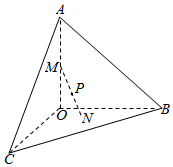 已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为4,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为$\frac{π}{6}$或$\frac{32}{3}$-$\frac{π}{6}$.
已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为4,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为$\frac{π}{6}$或$\frac{32}{3}$-$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2-x1)≥f(2-x2) | B. | f(2-x1)=f(2-x2) | C. | f(2-x1)<f(2-x2) | D. | f(2-x1)≤f(2-x2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com