
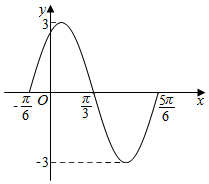
 如图是函数$f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<\frac{π}{2})$的图象的一部分.
如图是函数$f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<\frac{π}{2})$的图象的一部分.分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)由条件求得 $cos2α=\frac{1}{2}$,再根据 2α∈[π,2π],求得2α=$\frac{5π}{3}$,可得tan2α 的值.
解答 解:(1)由图象可知振幅A=3,又$T=\frac{5π}{6}-(-\frac{π}{6})=π$,∴ω=$\frac{2π}{T}=2$,∴f(x)=3sin(2x+φ).
再根据五点法作图可得 2•$\frac{π}{3}$+φ=π,∴$ϕ=\frac{π}{3}$,∴$f(x)=3sin(2x+\frac{π}{3})$.
(2)∵$f(α+\frac{π}{12})=\frac{3}{2}$,∴$3sin(2α+\frac{π}{2})=\frac{3}{2}$,∴$cos2α=\frac{1}{2}$.
∵α∈[$\frac{π}{2}$,π],∴2α∈[π,2π],∴2α=$\frac{5π}{3}$,∴tan2α=tan$\frac{5π}{3}$=tan(-$\frac{π}{3}$)=-tan$\frac{π}{3}$=-$\sqrt{3}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,根据三角函数的值求角,属于基础题.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,+∞] | B. | ($\frac{1}{2}$,1) | C. | ($\frac{1}{2}$,1] | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
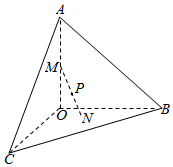 已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为4,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为$\frac{π}{6}$或$\frac{32}{3}$-$\frac{π}{6}$.
已知三棱锥A-BCO,OA、OB、OC两两垂直且长度均为4,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为$\frac{π}{6}$或$\frac{32}{3}$-$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -log20122011 | B. | -1 | C. | (log20122011)-1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2-x1)≥f(2-x2) | B. | f(2-x1)=f(2-x2) | C. | f(2-x1)<f(2-x2) | D. | f(2-x1)≤f(2-x2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com