
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
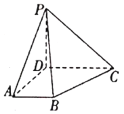
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .根据平面几何知识和线面垂直的判定可证得
.根据平面几何知识和线面垂直的判定可证得![]() 平面
平面![]() ,再证得
,再证得![]() ,可证明平面
,可证明平面![]() 平面
平面![]() .
.
(2)由线面角的定义可得![]() 为
为![]() 与平面
与平面![]() 所成的角,再以点
所成的角,再以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系,求得平面
轴,建立如图所示的空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,由二面角的向量求解方法可求得二面角
的法向量,由二面角的向量求解方法可求得二面角![]() 的余弦值.
的余弦值.
解:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
又∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为正方形,则
为正方形,则![]() .
.
∵![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∴![]() 平面
平面![]() .又
.又![]()
![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,∴
,∴![]() 为
为![]() 与平面
与平面![]() 所成的角,
所成的角,
即![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量
的一个法向量![]() .
.
设平面![]() 的法向量
的法向量![]() ,∵
,∵![]() ,
,![]() ,
,
则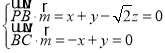 ,取
,取![]() ,则
,则![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,∴
,∴![]() .
.
由图可知二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x+1|.
(1)解关于x的不等式f(x)≤5;
(2)若函数f(x)的最小值记为m,设a,b,c均为正实数,且a+4b+9c=m,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
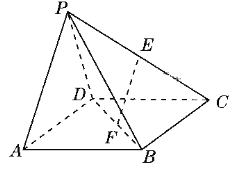
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某苗木基地常年供应多种规格的优质树苗.为更好地销售树苗,建设生态文明家乡和美好家园,基地积极主动地联系了甲、乙、丙三家公司,假定基地得到公司甲、乙、丙的购买合同的概率分别![]() 、
、![]() 、
、![]() ,且基地是否得到三家公司的购买合同是相互独立的.
,且基地是否得到三家公司的购买合同是相互独立的.
(1)若公司甲计划与基地签订300棵银杏实生苗的销售合同,每棵银杏实生苗的价格为90元,栽种后,每棵树苗当年的成活率都为0.9,对当年没有成活的树苗,第二年需再补种1棵.现公司甲为苗木基地提供了两种售后方案,
方案一:公司甲购买300棵银杏树苗后,基地需提供一年一次,共计两年的补种服务,且每次补种人工及运输费用平均为800元;
方案二:公司甲购买300棵银杏树苗后,基地一次性地多给公司甲60棵树苗,后期的移栽培育工作由公司甲自行负责.
若基地首次运送方案一的300棵树苗及方案二的360棵树苗的运费及栽种费用合计都为1600元,试估算两种方案下苗木基地的合同收益分别是多少?
(2)记![]() 为该基地得到三家公司购买合同的个数,若
为该基地得到三家公司购买合同的个数,若![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 平面
平面![]() ,且
,且![]() .
.
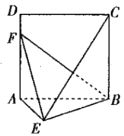
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二而角
,使二而角![]() 等于45°?若存在,请找出点
等于45°?若存在,请找出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为![]() ,
,

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,问在
两点,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?证明你的结论.
为定值?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com