
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
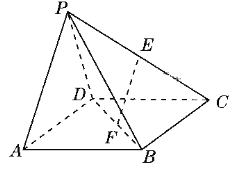
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据直线与平面平行的判定定理可知只需证![]() 与平面
与平面![]() 内一直线平行,连接
内一直线平行,连接![]() ,根据中位线可知
,根据中位线可知![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)根据面面垂直的性质可得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(3)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,从而得到
,从而得到![]() 平面
平面![]() ,即为四棱锥的高,最后根据棱锥的体积公式即可得解.
,即为四棱锥的高,最后根据棱锥的体积公式即可得解.
(1)如图所示,连接![]() .
.
∵四边形![]() 为矩形且
为矩形且![]() 是
是![]() 的中点,
的中点,
∴![]() 也是
也是![]() 的中点.
的中点.
又![]() 是
是![]() 的中点,
的中点,![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
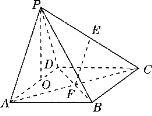
(2)证明:∵面![]() 平面
平面![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(3)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
∵平面![]() 平面
平面![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高,
的高,
∵![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴四棱锥![]() 的体积
的体积![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知点S为正方形ABCD所在平面外一点,△SBC是边长为2的等边三角形,点E为线段SB的中点.
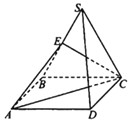
(1)证明:SD//平面AEC;
(2)若侧面SBC⊥底面ABCD,求平面ACE与平面SCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() .
.
(1)求椭圆C的离心率;
(2)设![]() 分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线
分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线![]() 相交于点M,N.当点P运动时,以M,N为直径的圆是否经过
相交于点M,N.当点P运动时,以M,N为直径的圆是否经过![]() 轴上的定点?试证明你的结论.
轴上的定点?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以平面直角坐标系的原点
为参数),以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,将曲线
轴的非负半轴为极轴建立极坐标系,将曲线![]() 绕极点顺时针旋转
绕极点顺时针旋转![]() 后得到曲线的曲线记为
后得到曲线的曲线记为![]() .
.
(1)求曲线![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】笔、墨、纸、砚是中国独有的文书工具,即文房四宝.笔、墨、纸、砚之名,起源于南北朝时期,其中“纸”指的是宣纸,“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸,宣纸按质量等级分类可分为正牌和副牌(优等品和合格品)某公司生产的宣纸为纯手工制作,年产宣纸10000刀,该公司按照某种质量指标x给宣纸确定质量等级,如下表所示:
x的范围 |
|
|
|
质量等级 | 正牌 | 副牌 | 废品 |
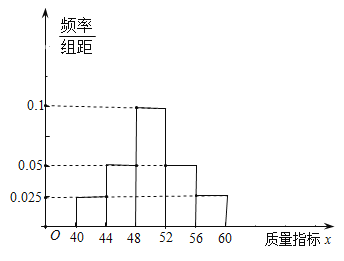
公司在所生产的宣纸中随机抽取了一刀(100张)进行检验,得到的频率分布直方图如上图所示.已知每张正牌宣纸的利润为12元,副牌宣纸的利润为6元,废品宣纸的利润为-12元.
(1)试估计该公司生产宣纸的利润;
(2)该公司预备购买一种售价为100万元的机器改进生产工艺,这种机器使用寿命为一年,不影响产量,这种机器生产的宣纸的质量指标x服从正态分布![]() ,改进工艺后正牌和副牌宣纸的利润都将受到不同程度的影响,观测的数据如下表所示:
,改进工艺后正牌和副牌宣纸的利润都将受到不同程度的影响,观测的数据如下表所示:
x的范围 |
|
| ||
一张宣纸的利润 | 12 | 8 | 8 | 3 |
频率 | 0.5 | 0.5 | 0.5 | 0.5 |
将频率视为概率,请判断该公司是否应该购买这种机器,并说明理由
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com