
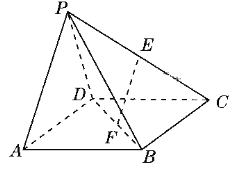
【题目】如图,已知点S为正方形ABCD所在平面外一点,△SBC是边长为2的等边三角形,点E为线段SB的中点.
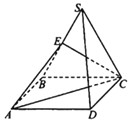
(1)证明:SD//平面AEC;
(2)若侧面SBC⊥底面ABCD,求平面ACE与平面SCD所成锐二面角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接BD交AC于F,连接EF,由已知结合三角形的中位线定理可得EF∥SD,再由直线与平面平行的判定可得SD∥平面AEC;
(2)取BC的中点O,连接OF并延长,可知OF⊥OC,利用线面垂直的判定定理与性质定理可得:OS⊥OF,OS⊥OC,建立空间直角坐标系,分别求出平面CDS与平面ACE的一个法向量,由两法向量所成角的余弦值可得平面ACE与平面SCD所成锐二面角的余弦值.
(1)证明:连接BD交AC于F,连接EF,
∵ABCD为正方形,F为BD的中点,且E为BS的中点,
∴EF∥SD.
又SD平面AEC,EF平面AEC,
∴SD∥平面AEC;
(2)取BC的中点O,连接OF并延长,可知OF⊥OC,
在等边三角形SBC中,可得SO⊥BC,
∵侧面SBC⊥底面ABCD,且侧面SBC∩底面ABCD=BC,
∴SO⊥平面ABCD,得OS⊥OF,OS⊥OC.
以O为坐标原点,分别以OF,OC,OS所在直线为x,y,z轴建立空间直角坐标系,
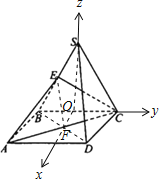
得:A(2,﹣1,0),C(0,1,0),E(0,![]() ,
,![]() ),D(2,1,0),S(0,0,
),D(2,1,0),S(0,0,![]() ).
).
![]() ,
,![]() ,
,![]() ,
,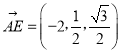 .
.
设平面CDS与平面ACE的一个法向量分别为![]() ,
,![]() .
.
由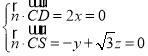 ,取z=1,得
,取z=1,得![]() ;
;
由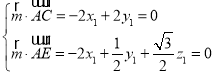 ,取x1=1,得
,取x1=1,得![]() .
.
∴cos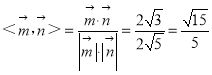 .
.
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
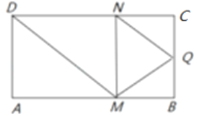
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上运动(其中
上运动(其中![]() 不与
不与![]() ,
,![]() 重合,
重合,![]() 不与
不与![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 将
将![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为______;当三棱锥
体积的最大值为______;当三棱锥![]() 体积最大时,其外接球的半径
体积最大时,其外接球的半径![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的曲线图是2020年1月25日至2020年2月12日陕西省及西安市新冠肺炎累计确诊病例的曲线图,则下列判断正确的是( )
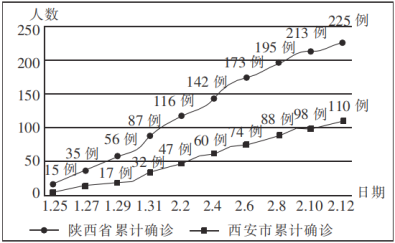
A.1月31日陕西省新冠肺炎累计确诊病例中西安市占比超过了![]()
B.1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了97例
D.2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率大于2月6日到2月8日的增长率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有报道称,据南方科技大学、上海交大等8家单位的最新研究显示:A、B、O、AB血型与COVID﹣19易感性存在关联,具体调查数据统计如图:

根据以上调查数据,则下列说法错误的是( )
A.与非O型血相比,O型血人群对COVID﹣19相对不易感,风险较低
B.与非A型血相比,A型血人群对COVID﹣19相对易感,风险较高
C.与O型血相比,B型、AB型血人群对COVID﹣19的易感性要高
D.与A型血相比,非A型血人群对COVID﹣19都不易感,没有风险
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x+1|.
(1)解关于x的不等式f(x)≤5;
(2)若函数f(x)的最小值记为m,设a,b,c均为正实数,且a+4b+9c=m,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com