
ЗжЮі ЧѓГіЯђСПЃЌРћгУЯђСПДЙжБЕФГфвЊЬѕМўЃЌСаГіЗНГЬЧѓНтМДПЩЃЎ
НтД№ НтЃКгЩЬѕМўЕУ$\overrightarrow{a}$=ЃЈ2ЃЌ1ЃЉЃЌ$\overrightarrow{b}$=ЃЈ3ЃЌ-2ЃЉЃЌ
$\overrightarrow{c}$=$\overrightarrow{a}$+k$\overrightarrow{b}$=ЃЈ2+3kЃЌ1-2kЃЉЃЌ$\overrightarrow{d}$=$\overrightarrow{a}$-$\overrightarrow{b}$=ЃЈ-1ЃЌ3ЃЉЃЌ
Ёп$\overrightarrow{c}$ЁЭ$\overrightarrow{d}$ЃЌ
ЁрЃЈ2-3kЃЉЁСЃЈ-1ЃЉ+ЃЈ1-2kЃЉЁС3=0ЃЌ
Ёр$k=\frac{1}{3}$ЃЎ
ЕуЦР БОЬтПМВщЯђСПДЙжБЕФГфвЊЬѕМўЕФгІгУЃЌзјБъЕФзјБъдЫЫуЃЌЪЧЛљДЁЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
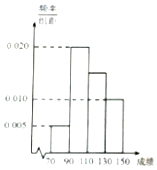 ФГАрбЇЩњвЛДЮЪ§бЇПМЪдГЩМЈЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌЪ§ОнЗжзщвРДЮЮЊ[70ЃЌ90ЃЉЃЌ[90ЃЌ110ЃЉЃЌ[110ЃЌ130ЃЉЃЌ[130ЃЌ150]ЃЌШєГЩМЈДѓгкЕШгк90ЗжЕФШЫЪ§ЮЊ36ЃЌдђГЩМЈдк[110ЃЌ130ЃЉЕФШЫЪ§ЮЊЃЈЁЁЁЁЃЉ
ФГАрбЇЩњвЛДЮЪ§бЇПМЪдГЩМЈЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌЪ§ОнЗжзщвРДЮЮЊ[70ЃЌ90ЃЉЃЌ[90ЃЌ110ЃЉЃЌ[110ЃЌ130ЃЉЃЌ[130ЃЌ150]ЃЌШєГЩМЈДѓгкЕШгк90ЗжЕФШЫЪ§ЮЊ36ЃЌдђГЩМЈдк[110ЃЌ130ЃЉЕФШЫЪ§ЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 12 | BЃЎ | 9 | CЃЎ | 15 | DЃЎ | 18 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 1 | BЃЎ | 2 | CЃЎ | 3 | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 0 | BЃЎ | 1 | CЃЎ | 2 | DЃЎ | 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com