
【题目】如图,在四棱柱![]() 中,四边形ABCD是边长等于2的菱形,
中,四边形ABCD是边长等于2的菱形,![]() ,
,![]() 平面ABCD,O,E分别是
平面ABCD,O,E分别是![]() ,AB的中点,AC交DE于点H,点F为HC的中点
,AB的中点,AC交DE于点H,点F为HC的中点
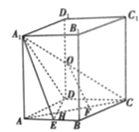
(1)求证:![]() 平面
平面![]() ;
;
(2)若OF与平面ABCD所成的角为60°,求三棱锥![]() 的表面积.
的表面积.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某处有一块闲置用地,如图所示,它的边界由圆O的一段圆弧![]() 和两条线段
和两条线段![]() ,
,![]() 构成.已知圆心O在线段
构成.已知圆心O在线段![]() 上,现测得圆O半径为2百米,
上,现测得圆O半径为2百米,![]() ,
,![]() .现规划在这片闲置用地内划出一片梯形区域用于商业建设,该梯形区域的下底为
.现规划在这片闲置用地内划出一片梯形区域用于商业建设,该梯形区域的下底为![]() ,上底为
,上底为![]() ,点M在圆弧
,点M在圆弧![]() (点D在圆弧
(点D在圆弧![]() 上,且
上,且![]() )上,点N在圆弧
)上,点N在圆弧![]() 上或线段
上或线段![]() 上.设
上.设![]() .
.
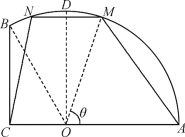
(1)将梯形![]() 的面积表示为
的面积表示为![]() 的函数;
的函数;
(2)当![]() 为何值时,梯形
为何值时,梯形![]() 的面积最大?求出最大面积.
的面积最大?求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱台ABC—DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC =2BC.
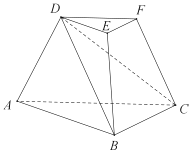
(I)证明:EF⊥DB;
(II)求DF与面DBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为![]() ,且
,且![]() ,定义X的信息熵
,定义X的信息熵![]() .( )
.( )
A.若n=1,则H(X)=0
B.若n=2,则H(X)随着![]() 的增大而增大
的增大而增大
C.若![]() ,则H(X)随着n的增大而增大
,则H(X)随着n的增大而增大
D.若n=2m,随机变量Y所有可能的取值为![]() ,且
,且![]() ,则H(X)≤H(Y)
,则H(X)≤H(Y)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
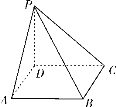
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】踢毽子是中国民间传统的运动项目之一,起源于汉朝,至今已有两千多年的历史,是一项简便易行的健身活动.某单位组织踢毽子比赛,把10人平均分成甲、乙两组,其中甲组每人在1分钟内踢毽子的数目分别为26,29,32,45,51;乙组每人在1分钟内踢毽子的数目分别为28,31,38,42,49.从甲、乙两组中各随机抽取1人,则这两人踢毽子的数目之和为奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
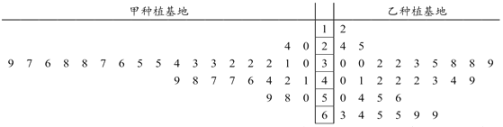
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com