
【题目】如图,已知抛物线![]() 焦点为
焦点为![]() ,过
,过![]() 上一点
上一点![]() 作切线
作切线![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() .
.

(1)证明:![]() ;
;
(2)设直线![]() ,
,![]() 的斜率为
的斜率为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的最小值.
的最小值.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中数学 来源: 题型:
【题目】斐波那契数列![]() 满足:
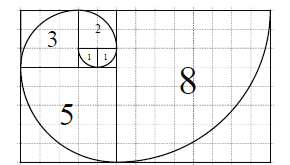
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为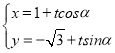 (a或t为参数).以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ
(a或t为参数).以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ![]() sinθ)=1.
sinθ)=1.
(1)当t为参数,α![]() 时,判断曲线C与直线l的位置关系;
时,判断曲线C与直线l的位置关系;
(2)当α为参数,t=2时,直线l与曲线C交于A,B两点,设P(1,0),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]()
![]() ,点
,点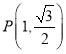 满足:
满足:![]() ,且
,且![]() .
.
(1)求椭圆C的标准方程;
(2)过点![]() 的直线l与C交于
的直线l与C交于![]() ,
,![]() 不同的两点,且
不同的两点,且![]() ,问在x轴上是否存在定点N,使得直线
,问在x轴上是否存在定点N,使得直线![]() ,
,![]() 与y轴围成的三角形始终为底边在y轴上的等腰三角形.若存在,求定点N的坐标;若不存在,请说明理由.
与y轴围成的三角形始终为底边在y轴上的等腰三角形.若存在,求定点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 在
在![]() 上的极值;
上的极值;
(3)设函数![]() ,若
,若![]() ,且对任意的实数
,且对任意的实数![]() ,不等式
,不等式![]() 恒成立(e是自然对数的底数),求实数a的取值范围.
恒成立(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如表:
送餐距离(千米) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
频数 | 15 | 25 | 25 | 20 | 15 |
以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表).
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
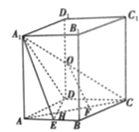
【题目】如图,在四棱柱![]() 中,四边形ABCD是边长等于2的菱形,
中,四边形ABCD是边长等于2的菱形,![]() ,
,![]() 平面ABCD,O,E分别是
平面ABCD,O,E分别是![]() ,AB的中点,AC交DE于点H,点F为HC的中点
,AB的中点,AC交DE于点H,点F为HC的中点
(1)求证:![]() 平面
平面![]() ;
;
(2)若OF与平面ABCD所成的角为60°,求三棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com