
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() (其中
(其中![]() ),且
),且![]() 的取值范围为
的取值范围为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)分类讨论,见解析(2)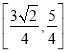
【解析】
(1)对函数进行求导,将导数的正负转化成研究一元二次函数的根的分布问题;
(2)利用韦达定理得到![]() ,
,![]() ,将
,将![]() 转化成关于
转化成关于![]() 的表达式,再利用换元法令
的表达式,再利用换元法令![]() ,从而构造函数
,从而构造函数![]() ,根据函数的值域可得自变量
,根据函数的值域可得自变量![]() 的范围,进而得到
的范围,进而得到![]() 的取值范围.
的取值范围.
解:(1)![]() .
.
令![]() ,则
,则![]() ,
,
①当![]() 或
或![]() ,即
,即![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() ,即
,即![]() 时,
时,
由![]() ,得
,得![]() 或
或![]() ;
;
由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
(2)由(1)得,当![]() 时,
时,![]() 有两极值点
有两极值点![]() ,
,![]() (其中
(其中![]() ).
).
由(1)得![]() ,
,![]() 为
为![]() 的两根,所以
的两根,所以![]() ,
,![]() .
.
所以![]()
![]() .
.
令![]() ,则
,则![]() ,
,
因为![]() ,
,
所以![]() 在
在![]() 上单调递减,而
上单调递减,而![]() ,
,![]() ,
,
所以![]() ,
,
又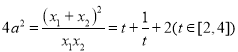 ,易知
,易知![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以实数![]() 的取值范围为
的取值范围为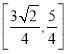 .
.


科目:高中数学 来源: 题型:
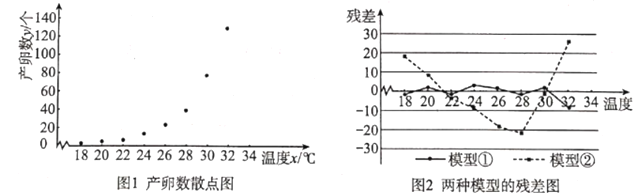
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为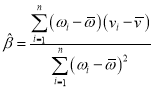 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 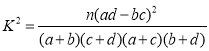 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 是两个焦点.以椭圆
是两个焦点.以椭圆![]() 的上顶点
的上顶点![]() 为圆心作半径为
为圆心作半径为![]() 的圆,
的圆,
(1)求椭圆![]() 的方程;
的方程;
(2)存在过原点的直线![]() ,与圆
,与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),使得
上),使得![]() ,求圆
,求圆![]() 半径
半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 与定点
与定点![]() 的距离和该动点到直线
的距离和该动点到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(1)求动点![]() 轨迹方程
轨迹方程![]() ;
;
(2)已知点![]() ,问在
,问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过
,使得过![]() 点的任一条斜率不为0的弦交曲线
点的任一条斜率不为0的弦交曲线![]() 于
于![]() 两点,都有
两点,都有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com