
分析 (Ⅰ)把要解的不等式转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.
(Ⅱ)当0<a<1时,在(0,+∞)上,不等式显然成立;当a>1时,结合f(x)、g(x)的图象,可得当g(x)的图象经过点(1,2)时,a=$\sqrt{2}$,要使不等式f(x)≥g(x)=loga(x+1)恒成立,a≥$\sqrt{2}$,综合可得,a的取值范围.
解答 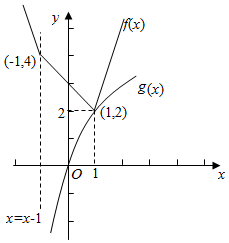 解:(Ⅰ)由于函数f(x)=|x+1|+2|x-1|,不等式f(x)≥x+3,即|x+1|+2|x-1|≥x+3,
解:(Ⅰ)由于函数f(x)=|x+1|+2|x-1|,不等式f(x)≥x+3,即|x+1|+2|x-1|≥x+3,
即 $\left\{\begin{array}{l}{x<-1}\\{-x-1+2(1-x)≥x+3}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{-1≤x<1}\\{x+1+2(1-x)≥x+3}\end{array}\right.$ ②,或$\left\{\begin{array}{l}{x≥1}\\{x+1+2(x-1)≥x+3}\end{array}\right.$③.
解①求得x<-1,解②求得-1≤x≤0,解③求得 x≥2,
故原不等式的解集为{x|x≤0,或x≥2}.
(Ⅱ)若关于x的不等式f(x)≥loga(x+1)在x≥0上恒成立,即|x+1|+2|x-1|≥loga(x+1)在x≥0上恒成立.
由于g(x)=loga(x+1)的图象经过点(0,0),且图象位于直线x=-1的右侧,
当0<a<1时,在(0,+∞)上,loga(x+1)<0,f(x)>0,不等式f(x)≥g(x)=loga(x+1)恒成立.
当a>1时,结合f(x)=$\left\{\begin{array}{l}{1-3x,x<-1}\\{3-x,-1≤x<1}\\{3x-1,x≥1}\end{array}\right.$、g(x)的图象,
当g(x)的图象经过点(1,2)时,a=$\sqrt{2}$,要使不等式f(x)≥g(x)=loga(x+1)恒成立,a≥$\sqrt{2}$,
综上可得,a的取值范围为(0,1)∪[2,+∞).
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,体现了数形结合、分类讨论的数学思想,属于中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
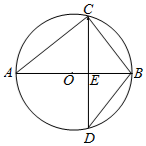 如图,AB是圆O的直径,CD是弦,CD⊥AB于点E,
如图,AB是圆O的直径,CD是弦,CD⊥AB于点E,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
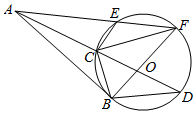 如图,AB是圆O的一条切线,切点为B,AF、AD都是圆O的割线,AD交圆O于点C,AF交圆O于点E,且∠ABC=∠ECF,连接EC、FB,BF过圆心O.
如图,AB是圆O的一条切线,切点为B,AF、AD都是圆O的割线,AD交圆O于点C,AF交圆O于点E,且∠ABC=∠ECF,连接EC、FB,BF过圆心O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com