练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若a>0，b>0，a＋b＝2，则下列不等式对一切满足条件的a，b恒成立的是________．(写出所有正确命题的编号)

    ①b≤1；②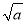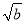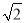＋≤；③a2＋b2≥2；④a3＋b3≥3；⑤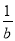＋≥2.

     

    ①③⑤

    【解析】对于命题①，由2＝a＋b≥2，得ab≤1，命题①正确；对于命题②，当a＝b＝1时，不成立，∴命题②错误；对于命题③，a2＋b2＝(a＋b)2－2ab＝4－2ab≥2，命题③正确；对于命题④，当a＝b＝1时，不成立，∴命题④错误；对于命题⑤，＋＝＝≥2，命题⑤正确．∴正确的结论为①③⑤.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-3空间点直线平面之间的位置关系（解析版） 题型：填空题

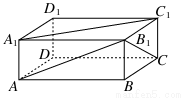
    如图所示，ABCD－A1B1C1D1是长方体，AA1＝a，∠BAB1＝∠B1A1C1＝30°，则AB与A1C1所成的角为________，AA1与B1C所成的角为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-6直接证明与间接证明（解析版） 题型：填空题

    请阅读下列材料：若两个正实数a1，a2满足a12＋a22＝1，那么a1＋a2≤.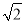

    证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.

    根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-5合情推理与演绎推理（解析版） 题型：选择题

    给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：

    ①“若a，b∈R，则a－b＝0⇒a＝b”，类比推出“若a，b∈C，则a－b＝0⇒a＝b”；

    ②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”，类比推出，“若a，b，c，d∈Q，则a＋b＝c＋d⇒a＝c，b＝d”；

    ③“若a，b∈R，则a－b>0⇒a>b”，类比推出“若a，b∈C，则a－b>0⇒a>b”；

    ④“若x∈R，则|x|<1⇒－1<x<1”，类比推出“若z∈C，则|z|<1⇒－1<z<1”．

    其中类比正确的为(　　)

    A．①② B．①④ C．①②③ D．②③④

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：选择题

    已知a>0，b>0，若不等式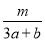－－≤0恒成立，则m的最大值为(　　)

    A．4 B．16 C．9 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-4基本不等式（解析版） 题型：选择题

    若向量a＝(x－1,2)，b＝(4，y)相互垂直，则9x＋3y的最小值为(　　)

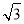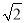    A．12 B．2 C．3 D．6

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-2一元二次不等式及其解法（解析版） 题型：解答题

    设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．

    (1)若m＝－1，n＝2，求不等式F(x)>0的解集；

    (2)若a>0，且0<x<m<n<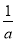，比较f(x)与m的大小．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：6-1不等关系与不等式（解析版） 题型：解答题

    已知关于x的不等式(ax－5)(x2－a)<0的解集为M.

    (1)当a＝4时，求集合M；

    (2)当3∈M，且5∉M时，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：5-3等比数列及其前n项和（解析版） 题型：选择题

    已知各项为正的等比数列{an}中，a4与a14的等比中项为2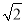，则2a7＋a11的最小值为(　　)

    A．16 B．8 C．6 D．4

     

    查看答案和解析>>

    同步练习册答案