【题目】已知函数
.
（1）求函数
的单调区间；
（2）若
，关于
的方程
有三个不同的实根，求
的取值范围.
【答案】（1）见解析（2）
【解析】试题分析：（1）先求函数的定义域。再求导函数，令导函数大于、小于0，求单调区间。解不等式时讨论
与0、1的大小。（2）关于
的方程
有三个不同的实根，转化为方程
有三个不同的实根。若
，由（1）可求
的单调区间，进而求其最大、最小值， 
大于最小值、小于最大值。
试题解析：（1）函数
的定义域是
.
.
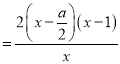①当
时， 
在
上恒成立， 
在
上恒成立，
时， 
的增区间为
， 
的减区间为
.
②当
时， 
在
和
上恒成立.
在
上恒成立.
时， 
的增区间为
和
， 
的减区间为
.
③当
时， 
在
上恒成立，
时， 
的增区间为
.
④当
时， 
在
和
上恒成立， 
在
上恒成立，
时， 
的增区间为
和
， 
的减区间为
.
（2）若
，由（1）可得
在
上当调递增，在
上单调递减，在
上单调递增.
， 
，
的图象与直线
有三个交点时
的取值范围是
.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各10件样品，测量产品中某种元素的含量（单位：毫克），如图是测量数据的茎叶图：
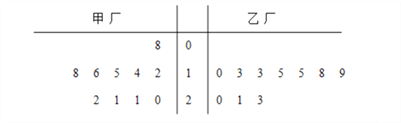
规定：当产品中的此种元素含量不小于16毫克时，该产品为优等品．
（1）从乙厂抽出的上述10件样品中，随机抽取3件，求抽到的3件样品中优等品数
的分布列及其数学期望
；
（2）从甲厂的10件样品中有放回地逐个随机抽取3件，也从乙厂的10件样品中有放回地逐个随机抽取3件，求抽到的优等品数甲厂恰比乙厂多2件的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
.
（1）求函数
的单调区间；
（2）当
时，是否存在整数
，使不等式
恒成立？若存在，求整数
的值；若不存在，则说明理由；
（3）关于
的方程
在
上恰有两个相异实根，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝
(1) 判别函数f(x)的奇偶性；
(2) 判断函数f(x)的单调性，并根据函数单调性的定义证明你的判断正确；
(3) 求关于x的不等式f(1－x2)＋f(2x＋2)＜0的解集．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
，
，
）．
（1）若
的部分图像如图所示，求
的解析式；
（2）在（1）的条件下，求最小正实数
，使得函数
的图象向左平移
个单位后所对应的函数是偶函数；
（3）若
在
上是单调递增函数，求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱柱ABC-A1B1C1中，侧棱垂直于底面,AC=BC,点D是AB的中点．
(1)求证：BC1∥平面CA1D；(2)若底面ABC为边长为2的正三角形，BB1=
求三棱锥B1-A1DC的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
