
|
| ��n������ |
| ǰn-1����Ͷ����ʽ��ܺ� |
| 1 |
| 5 |
| n(1+n) |
| 2 |
| n(1+n) |
| 10 |
| 12•13 |
| 10 |
| 5 |
| 2 |
| 5 |
| 2 |
| 72 |
| 5 |
|
| n |
| 5 |
| (n-1)(n-2) |
| 2 |
| n(n-1) |
| 20 |
| ||
5+
|
| 4 | ||
|
| 1 |
| 25 |
| 4 |
| 19 |
| 5 |
| 2 |
| (n-1)(n-2) |
| 2 |
| n(n-1) |
| 20 |
| ||
5+
|
| 25 |
| 326 |
| 25 |
| 128 |
| 4 |
| 19 |
| 25 |
| 128 |
| 4 |
| 19 |


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2n |
| an•an+1 |
| 1 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| an2 |
| 4an2+1 |
| Sn+1 |
| an2 |
| Sn |
| an+12 |
| m |
| 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
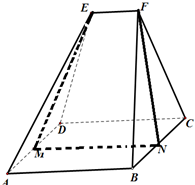 ľ���������ҹ���ͳ�Ļ��屦֮һ���������Ͷ�����������ǻۣ��ܶ�Ŵ������ͼҾ߲������������浽�ִ�ȴ��Ȼ�ι̣������У������Ӽӹ̹��ܵġ�Ш�ӡ���������Ҫ���ã���ͼ����һ��Ш����״��ֱ��ͼ�������ABCDΪһ�����Σ�����AB=6��AD=4�������߶�EF��ƽ��ABCD����EA=ED=FB=FC=6
ľ���������ҹ���ͳ�Ļ��屦֮һ���������Ͷ�����������ǻۣ��ܶ�Ŵ������ͼҾ߲������������浽�ִ�ȴ��Ȼ�ι̣������У������Ӽӹ̹��ܵġ�Ш�ӡ���������Ҫ���ã���ͼ����һ��Ш����״��ֱ��ͼ�������ABCDΪһ�����Σ�����AB=6��AD=4�������߶�EF��ƽ��ABCD����EA=ED=FB=FC=6| 2 |
| ||
| 17 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A1An+1 |
| BnCn |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
-
| ||
ax+
|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com