
| 1 |
| 2 |
| 1 |
| 2 |
| x2+(y-2)2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.
某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.| A、11 | B、13 | C、15 | D、17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
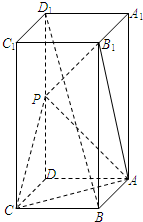 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=2AB,且点P为DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=2AB,且点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
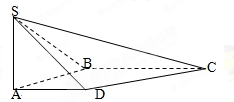 在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=
在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| Sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:
在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:| x2 |
| a2 |
| y2 |
| 3 |
| PB |
| PA |
| B′F |
| FA |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 第n月利润 |
| 前n-1个月投入的资金总和 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com