
分析 (Ⅰ)求出函数的导数,计算f′(1),f(1)的值,代入切线方程即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,确定函数的单调区间即可;
(Ⅲ)问题转化为f(x)max<0,结合函数的单调性,求出函数的最大值,从而求出a的范围.
解答 解:( I)由已知:a=2时,f(x)=lnx-2x,(x>0),
∴$f'(x)=\frac{1}{x}+2,(x>0)$,
f′(1)=3所以斜率k=3,f(1)=2,
又切点为(1,2),所以切线方程为y-2=3(x-1),
即3x-y-1=0; …(2分)
( II)$f'(x)=\frac{1}{x}-a=\frac{1-ax}{x},(x>0)$
①当a≤0时,由于x>0,得:1-ax>0,f′(x)>0,
所以f(x)的单调递增区间为(0,+∞),…(4分)
②当a>0时,f′(x)=0,得$x=\frac{1}{a}$,
在区间$(0,\frac{1}{a})$上,f′(x)>0,
在区间$(\frac{1}{a},+∞)$上,f′(x)<0,
所以f(x)的单调递增区间为$(0,\frac{1}{a})$,
单调递减区间为$(\frac{1}{a},+∞)$; …(8分)
( III)由已知,转化为f(x)max<0,
由( II)知,当a≤0时,f(x)在(0,+∞)单调递增,值域为R,
不符合题意,
当a>0时,f(x)在$(0,\frac{1}{a})$单调递增,f(x)在$(\frac{1}{a},+∞)$单调递减,
所以f(x)的极大值即为最大值,$f(\frac{1}{a})=ln(\frac{1}{a})-1=-lna-1$,
所以-lna-1<0,解得:$a>\frac{1}{e}$.…(12分)
点评 本题考查了曲线的切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sinxcosx | B. | y=sin(2x+$\frac{π}{2}$) | C. | y=tan2x | D. | y=sin2x+cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
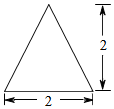 一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积是( )
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积是( )| A. | $4\sqrt{3}$ | B. | $4\sqrt{5}$ | C. | $4({\sqrt{5}+1})$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com