练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数h(x)＝2x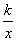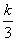－＋在(1，＋∞)上是增函数，则实数k的取值范围是(    )．

    Ａ．[1，＋∞)          Ｂ． (－2，＋∞)        Ｃ．[－2，2]     Ｄ． [－2，＋∞)


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    执行如右上图所示的程序框图，输出的值为(   )

    A．             B．C．                D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题 “自然数a、b 、c中恰有一个偶数”时，需假设原命题不成立，下列假设正确的是（    ）

    A．a、b、c都是奇数                        B．a、b 、c都是偶数

    C．a、b、c中或都是奇数或至少有两个偶数    D．a、b 、c中至少有两个偶数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


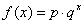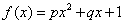    某地区的一种特色水果上市时间仅能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格下跌．经市场分析，价格模拟函数为以下三个函数中的一个：①；②；③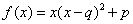．（以上三式中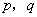均为常数，且）（注：函数的定义域是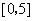）．其中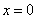表示4月1日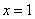，表示5月1日，…，依此类推.

    （Ⅰ）请判断以上哪个价格模拟函数能准确模拟价格变化走势，为什么？

    （Ⅱ）若该果品4月1日投入市场的初始价格定为6元，且接下来的一个月价格持续上涨，并在5 月1日达到了一个最高峰，求出所选函数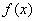的解析式；

    （Ⅲ）在（Ⅱ）的条件下，为保护果农的收益，打算在价格下跌期间积极拓宽境外销售，且销售价格为该果品上市期间最低价格的2倍，请你预测该果品在哪几个月内价格下跌及境外销售的价格．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，当时，（　）

    Ａ．        Ｂ．         Ｃ．        Ｄ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


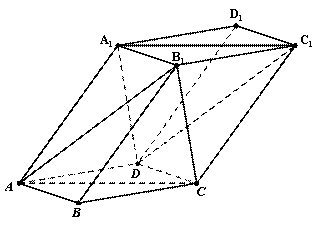
    如图，棱柱ABCD－A1B1C1D1的底面ABCD为菱形，四边形AA1C1C也为菱形

    且∠A1AC=∠DAB=60o，平面AA1C1C⊥平面ABCD.（Ⅰ）证明：BD⊥AA1；

    （Ⅱ）证明：平面AB1C∥平面DA1C1；

    （Ⅲ）在棱CC1上是否存在点P，使得平面PDA1和平面DA1C1所成锐二面角的余弦值为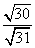？若存在，求出点P的位置；若不存在，说明理由．

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列1，2，3，4，5，6，……，按如下规则构造新数列：1，（2+3），（4+5+6），（7+8+9+10），……，  则新数列的第n项为_________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆上一点P到椭圆的一个焦点的距离等于4，那么点P到另一个焦点的距离等于          ．

    查看答案和解析>>

    同步练习册答案