
分析 (1)设v(x)=ax+b.利用x的范围,列出方程组求解a,b,即可得到函数的解析式.
(2)求出车流量f(x)=v(x)•x的表达式,然后求解最大值即可.
解答 解:(1)由题意,得当0≤x≤20时,v(x)=60;
当20≤x≤200时,
设v(x)=ax+b.
由已知$\left\{\begin{array}{l}200a+b=0\\ 20a+b=60\end{array}\right.$,解得$\left\{\begin{array}{l}a=-\frac{1}{3}\\ b=\frac{200}{3}\end{array}\right.$,
故函数v(x)的表达式为v(x)=$\left\{\begin{array}{l}60,0≤x≤20\\ \frac{1}{3}(200-x),20<x≤200\end{array}\right.$
(2)$f(x)=v(x)•x=\left\{\begin{array}{l}60x,0≤x≤20\\-\frac{1}{3}{(x-100)^2}+\frac{10000}{3},20<x≤200\end{array}\right.$,
当0≤x≤20时,f(x)1200.
当20<x≤200时,$-\frac{1}{3}{(x-100)}^{2}+\frac{10000}{3}≤\frac{10000}{3}$.
所以$f{(x)_{max}}=f(100)=\frac{10000}{3}$.
点评 本题考查函数模型的选择与应用,二次函数的性质以及最值的求法,分段函数的应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=AP,PA⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB=AP,PA⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
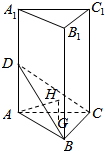 如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.
如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com