Question

【题目】已知在数列{an}中，设a1为首项，其前n项和为Sn，若对任意的正整数m，n都有不等式S2m+S2n＜2Sm+n（m≠n）恒成立，且2S6＜S3．

（1）设数列{an}为等差数列，且公差为d，求的取值范围；

（2）设数列{an}为等比数列，且公比为q（q＞0且q≠1），求a1q的取值范围．

Answer 1

【答案】(1)＜﹣3；（2）a1q＞0

【解析】

（1）根据已知条件，由于数列是等差数列，运用等差数列的求和公式，建立不等式，进一步求出相应的结果；

（2）根据已知条件，由于数列是等比数列，运用等比数列的求和公式，建立不等式，进一步求出相应的结果．

在数列{an}中，设a1为首项，其前n项和为Sn，

若对任意的正整数m、n都有不等式S2m+S2n＜2Sm+n（m≠n）恒成立，

（1）设{an}为等差数列，且公差为d，

则：2ma1+d+2na1+d＜2[（m+n）a1+d]，

整理得：（m﹣n）2d＜0，则d＜0，由2S6＞S3，整理得：9a1+27d＞0，

则a1＞﹣3d，所以d＜0，＜﹣3；

（2）设{an}为等比数列，且公比为q（q＞0且q≠1），

则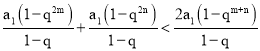，整理得（2qm+n﹣q2m﹣q2n）＜0，

则：﹣（qm﹣qn）2＜0，所以＞0，由2S6＞S3，则：2q6﹣q3﹣1＜0

解得：﹣＜q3＜1，由于q＞0，所以：0＜q＜1，则：a1＞0．即有a1q＞0．