
分析 根据题意,利用同角的三角函数关系和两角和与差的公式,求出cos(B-C)=-$\frac{1}{2}$,
再求出cos2A+cos2B+cos2C=0,利用降幂公式即可求出cos2A+cos2B+cos2C的值.
解答 证明:由sinA=-(sinB+sinC),cosA=-(cosB+cosC),
sin2A+cos2A=1,
∴(sinB+sinC)2+(cosB+cosC)2=1,
sin2B+2sinBsinC+sin2C+cos2B+2cosBcosC+cos2C=1,
2+2cos(B-C)=1
即cos(B-C)=-$\frac{1}{2}$,
∴cos2A+cos2B+cos2C=2cos2A-1+cos2B+cos2C,
=2cos2B+2cos2C-1+4cosBcosC+cos2B+cos2C,
=2cos2B+2cos2C+4cosBcosC+1,
=4cos(B+C)cos(B-C)+2[cos(B+C)+cos(B-C)]+1,
=-2cos(B+C)+2cos(B+C)-1+1,
=0;
∴cos2A+cos2B+cos2C=$\frac{1+cos2A}{2}$+$\frac{1+cos2B}{2}$+$\frac{1+cos2C}{2}$
=$\frac{3}{2}$+$\frac{1}{2}$(cos2B+cos2B+cos2C)=$\frac{3}{2}$.
点评 本题考查同角的基本关系,两角和差的正余弦公式及二倍角公式,证明过程复杂,需要敏锐的观察能力,属于中档题.


科目:高中数学 来源: 题型:解答题
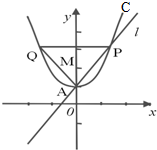 已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.
已知二次函数y=ax2+1的图象为抛物线C,过顶点A(0,1)的直线l与抛物线C相交于另外一点P,点Q为抛物线C上另外一点,且点M(0,m)到直线l的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64 | B. | 100 | C. | 36 | D. | 136 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在x=1处取到极大值 | B. | f(x)在x=1处取到极小值 | ||
| C. | f(x)在x=0处取到极大值 | D. | f(x)在x=0处取到极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
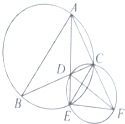 如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.
如图,在△ABC中,∠BAC的平分线交BC于点D,交△ABC的外接圆于点E,延长AC交△DCE的外接圆于点F,DF=$\sqrt{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com