
【题目】已知椭圆C1: ![]() +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上, ![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】
(1)解:椭圆 ![]() 的长轴长为4,离心率为
的长轴长为4,离心率为 ![]()
∵椭圆C2以C1的长轴为短轴,且与C1有相同的离心率
∴椭圆C2的焦点在y轴上,2b=4,为 ![]()
∴b=2,a=4
∴椭圆C2的方程为 ![]()
(2)解:设A,B的坐标分别为(xA,yA),(xB,yB),
∵ ![]()
∴O,A,B三点共线,且点A,B不在y轴上
∴设AB的方程为y=kx
将y=kx代入 ![]() ,消元可得(1+4k2)x2=4,∴
,消元可得(1+4k2)x2=4,∴ ![]()
将y=kx代入 ![]() ,消元可得(4+k2)x2=16,∴
,消元可得(4+k2)x2=16,∴ ![]()
∵ ![]() ,∴
,∴ ![]() =4
=4 ![]() ,
,
∴ ![]() ,解得k=±1,
,解得k=±1,
∴AB的方程为y=±x
【解析】(1)求出椭圆 ![]() 的长轴长,离心率,根据椭圆C2以C1的长轴为短轴,且与C1有相同的离心率,即可确定椭圆C2的方程;(2)设A,B的坐标分别为(xA , yA),(xB , yB),根据
的长轴长,离心率,根据椭圆C2以C1的长轴为短轴,且与C1有相同的离心率,即可确定椭圆C2的方程;(2)设A,B的坐标分别为(xA , yA),(xB , yB),根据 ![]() ,可设AB的方程为y=kx,分别与椭圆C1和C2联立,求出A,B的横坐标,利用
,可设AB的方程为y=kx,分别与椭圆C1和C2联立,求出A,B的横坐标,利用 ![]() ,即可求得直线AB的方程.
,即可求得直线AB的方程.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合U=R,A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求A∩B,(UA)∪B;
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .若点
.若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.
的一个“椭点”.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,
, ![]() ,以
,以![]() 为直径的圆经过坐标原点,试求
为直径的圆经过坐标原点,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ ![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线L:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣ ![]() ,求证:△AOB的面积为定值.
,求证:△AOB的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为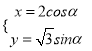 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com