
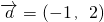 ,又点A(8,0),B(n,t),C(ksinθ,t).
,又点A(8,0),B(n,t),C(ksinθ,t).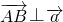 ,且
,且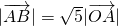 ,求向量
,求向量 .
. 与向量
与向量 共线,常数k>0,当f(θ)=tsinθ取最大值4时,求
共线,常数k>0,当f(θ)=tsinθ取最大值4时,求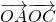 .
.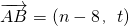 ,∵
,∵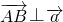 ,∴8-n+2t=0
,∴8-n+2t=0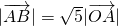 ,∴(n-8)2+t2=5×64得t=±8∴
,∴(n-8)2+t2=5×64得t=±8∴ 或(-8,-8)
或(-8,-8) ,
, 与向量
与向量 共线,
共线,
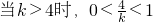 ∴
∴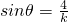 时,tsinθ取最大值为
时,tsinθ取最大值为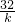 ,
,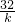 =4,得k=8,此时
=4,得k=8,此时 ,
,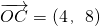
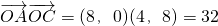
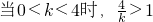 ,
,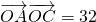
 与向量
与向量 共线,得出f(θ)=tsinθ=(-2ksinθ+16)sinθ,根据最大值4,求出k或θ,求
共线,得出f(θ)=tsinθ=(-2ksinθ+16)sinθ,根据最大值4,求出k或θ,求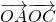 .
.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com