
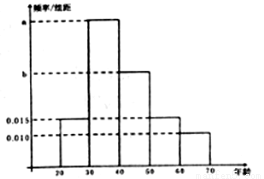
(本小题满分12分)根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如下图显示.
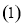 已知
已知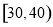 、
、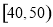 、
、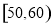 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
,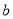 的值;
的值;
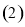 该电子商务平台将年龄在
该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和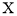 的分布列与数学期望.
的分布列与数学期望.
(1)  ,
, ;(2)
;(2)
| 150 | 200 | 250 | 300 |
|
|
|
|
|
 .
.
【解析】
试题分析:(1)根据频率直方图中结论:所有频率之和为1,则有: ,即有:
,即有: ,又由条件:
,又由条件: 、
、 、
、 三个年龄段的上网购物者人数成等差数列,则有:
三个年龄段的上网购物者人数成等差数列,则有: ,解方程组得:
,解方程组得: ,
, ;(2) 根据(1)中:
;(2) 根据(1)中: ,可得高消费人群所占比例为
,可得高消费人群所占比例为 ,利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人.从中取出三人,并计算三人所获得代金券的总和
,利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人.从中取出三人,并计算三人所获得代金券的总和 ,则
,则 的所有可能取值为:150,200,250,300. 运用概率公式求得:
的所有可能取值为:150,200,250,300. 运用概率公式求得: ,
, ,
, ,
, ,用列表的形式即可得到概率分布表,运用数学期望公式求得:
,用列表的形式即可得到概率分布表,运用数学期望公式求得: .
.
试题解析:(1)由图可知 ,
, . (4分)
. (4分)
(2) 利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人. (6分)
从中取出三人,并计算三人所获得代金券的总和 ,
,
则 的所有可能取值为:150,200,250,300.
的所有可能取值为:150,200,250,300.
 ,
,  ,
,
 ,
,  ,
,
| 150 | 200 | 250 | 300 |
|
|
|
|
|
(10分)
且 . (12分)
. (12分)
考点:1.统计与概率的相关知识;2.离散型随机变量的分布列;3.数学期望


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年重庆市高二上学期第三次月考理科数学试卷(解析版) 题型:解答题
(本小题12分)如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB//DC, ,PA
,PA 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=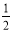 AB=1,M是PB的中点。
AB=1,M是PB的中点。

(1)证明:面PAD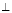 面PCD;
面PCD;
(2)求AC与PB所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系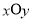 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(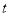 为参数),以原点
为参数),以原点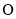 为极点,以
为极点,以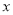 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线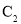 的极坐标方程为
的极坐标方程为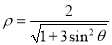 .
.
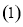 求曲线
求曲线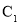 的普通方程与曲线
的普通方程与曲线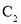 的直角坐标方程;
的直角坐标方程;
 试判断曲线
试判断曲线 与
与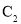 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)文科数学试卷(解析版) 题型:选择题
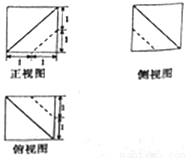
一个几何体的三视图如图所示,则该几何体的体积为( )
A.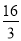 B.
B.
C.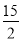 D.
D.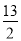
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系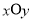 中,曲线
中,曲线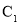 的参数方程为
的参数方程为 (
(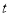 为参数),以原点
为参数),以原点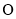 为极点,以
为极点,以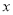 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线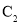 的极坐标方程为
的极坐标方程为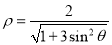 .
.
 求曲线
求曲线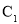 的普通方程与曲线
的普通方程与曲线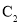 的直角坐标方程;
的直角坐标方程;
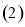 试判断曲线
试判断曲线 与
与 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)理科数学试卷(解析版) 题型:选择题
一个几何体的三视图如图所示,则该几何体的体积为( )
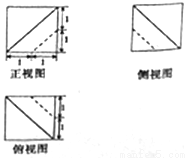
A.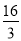 B.
B.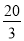
C.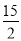 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:选择题
定义在R上的函数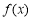 满足
满足 ,当
,当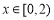 时,
时, 函数
函数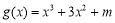 .若
.若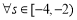 ,
,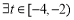 ,不等式
,不等式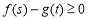 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( )
(A)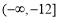 (B)
(B)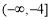
(C) (D)
(D)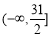
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:填空题
已知 分别为双曲线
分别为双曲线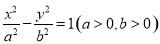 的左,右焦点,P为双曲线右支上的一点,且
的左,右焦点,P为双曲线右支上的一点,且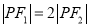 .若
.若 为等腰三角形,则该双曲线的离心率为_________.
为等腰三角形,则该双曲线的离心率为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com