
分析 (1)利用向量的垂直关系,化简求解即可.
(2)利用两角和的正弦函数化简,通过正弦函数的单调性求解即可.
(3)利用三角形的面积,以及两角和的正弦函数求解范围即可.
解答 解:(1)∵$\overrightarrow m$=(2sinB,$\sqrt{3}$),$\overrightarrow n$=(${2{{cos}^2}\frac{B}{2}$-1,cos2B),$\overrightarrow{m}⊥\overrightarrow{n}$,
∴2sinBcosB+$\sqrt{3}$cos 2B=0,即sin2B=-$\sqrt{3}$cos2B,
∴tan2B=-$\sqrt{3}$,又B为锐角,∴2B∈(0,π),
∴2B=$\frac{2π}{3}$,B=$\frac{π}{3}$,
(2)∴f(x)=sin2xcosB-cos2xsinB=sin(2x-$\frac{π}{3}$).
令-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{π}{2}$+2kπ(k∈Z),
解得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$(k∈Z),
∴函数f(x)的单调递增区间是:[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z),
(3)由(1)知B=$\frac{π}{3}$,b=4,
∵$S△ABC=\frac{1}{2}acsinB=\frac{{16\sqrt{3}}}{3}sinAsin(\frac{2π}{3}-A)$=$\frac{{8\sqrt{3}}}{3}sin({2A-\frac{π}{6}})+\frac{{4\sqrt{3}}}{3}$
∵$A∈({\frac{π}{6},\frac{π}{2}})$,
∴$S△ABC∈({\frac{{4\sqrt{3}}}{3},4\sqrt{3}}]$.
点评 本题考查两角和与差的三角函数,向量的数量积的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | {x|-4<x<-1} | B. | {x|-1≤x<2} | C. | {x|-4<x≤-1} | D. | {x|-1≤x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
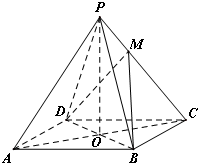 如图,已知四棱锥P-ABCD,底面对角线AC,BD交于点O,$\overrightarrow{AB}=\overrightarrow{DC}且\overrightarrow{AC}•(\overrightarrow{DC}-\overrightarrow{BC})=0$,又知OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).
如图,已知四棱锥P-ABCD,底面对角线AC,BD交于点O,$\overrightarrow{AB}=\overrightarrow{DC}且\overrightarrow{AC}•(\overrightarrow{DC}-\overrightarrow{BC})=0$,又知OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$(λ>0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为k(k>0)的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为k(k>0)的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com