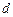练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    一颗慧星沿一条以地球为焦点的抛物线运行时，当慧星离地球万公里时，经过地球和慧得的直线与抛物线对称轴的夹角为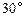，求此慧星运行时离地球的最近距离．
    慧星与地球距离最短为或（万公里）
    以慧星和地球最近点的连线所在轴为轴，

    最近点为原点建立坐标系，地球与抛物线焦点，
    此时抛物线方程为，
    由题设知点或在抛物线上．
    可求得或．
    慧星与地球的距离等于，
    故当时，慧星与地球距离最短为或（万公里）．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

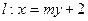    过点T（2，0）的直线交抛物线y2=4x于A、B两点.
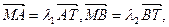    （I）若直线l交y轴于点M，且当m变化时，求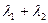的值；
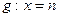    （II）设A、B在直线上的射影为D、E，连结AE、BD相交于一点N，则当m变化时，点N为定点的充要条件是n=－2.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知抛物线y2=-8mx(m>0),是否存在过抛物线的焦点F的弦PQ,使△POQ的面积最大或最小?若存在,求出PQ所在直线的倾斜角;若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    炮弹运行的轨道是抛物线,现测得我炮位A与目标B的水平距离为6 000米,已知当射程为6 000米时,炮弹运行的最大高度是1 200米,在A、B之间距离A点500米处有一高达350米的障碍物,试确定炮弹可否安全越过此障碍物.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    当0<k<时,方程=kx的解的个数是(    )
    A．3B．2C．1D．0

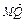    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知点P（-3，0），点A在y轴上，点Q在x轴非负半轴上，点M在直线AQ上，满足·=0，=-.
    （1）当点A在y轴上移动时，求动点M的轨迹C的方程；
    （2）设轨迹C的准线为l,焦点为F，过F作直线m交轨迹C于G，H两点，过点G作平行于轨迹C的对称轴的直线n,且n∩l=E，试问点E，O，H（O为坐标原点）是否在同一条直线上？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

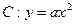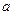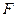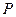    已知抛物线（为非零常数）的焦点为，点为抛物线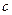上一个动点，过点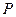且与抛物线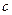相切的直线记为．
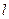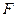    （1）求的坐标；
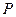    （2）当点在何处时，点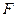到直线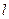的距离最小？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    将抛物线按向量平移后所得抛物线的焦点坐标为___________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    抛物线y2=4x关于直线x＋y=0对称的抛物线的方程是（   ）
    A．x2＝4yB．y2=－4xC．y=－4x2D．x2=－4y

    查看答案和解析>>

    同步练习册答案