
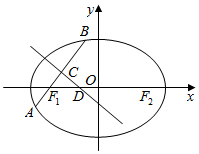
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{3}{2}$),且离心率为$\frac{1}{2}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{3}{2}$),且离心率为$\frac{1}{2}$.分析 (1)由题意知e=$\frac{c}{a}$=$\frac{1}{2}$,$\frac{1}{{a}^{2}}$+$\frac{\frac{9}{4}}{{b}^{2}}$=1,从而求椭圆C的方程;
(2)分类讨论,从而分别确定$\frac{|D{F}_{1}|}{|AB|}$=$\frac{1}{4}$;从而证明.当斜率存在且不为0时,设直线l的方程为y=k(x+1),k≠0;从而联立方程化简得(4k2+3)x2+8k2x+4k2-12=0,利用韦达定理求距离,从而求比值.
解答 解:(1)由题意知,
e=$\frac{c}{a}$=$\frac{1}{2}$,$\frac{1}{{a}^{2}}$+$\frac{\frac{9}{4}}{{b}^{2}}$=1,
解得,a=2,b=$\sqrt{3}$,c=1;
故椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)①当直线l的斜率为0时,|AB|=2a=4,
|DF1|=c=1,
故$\frac{|D{F}_{1}|}{|AB|}$=$\frac{1}{4}$;
②当直线l的斜率不存在时,|DF1|不存在,
故$\frac{|D{F}_{1}|}{|AB|}$不存在;
③设直线l的方程为y=k(x+1),k≠0;
与$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1联立消元可得:
(4k2+3)x2+8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$,
故|AB|=$\sqrt{1+{k}^{2}}$$•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{144({k}^{2}+1)}{(4{k}^{2}+3)^{2}}}$=$\frac{12({k}^{2}+1)}{4{k}^{2}+3}$;
$\frac{1}{2}$(x1+x2)=-$\frac{4{k}^{2}}{4{k}^{2}+3}$,$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{1}{2}$k(x1+x2)+k=$\frac{3k}{4{k}^{2}+3}$
故AB的中点的坐标为(-$\frac{4{k}^{2}}{4{k}^{2}+3}$,$\frac{3k}{4{k}^{2}+3}$),
故AB的中垂线的方程为y-$\frac{3k}{4{k}^{2}+3}$=-$\frac{1}{k}$(x+$\frac{4{k}^{2}}{4{k}^{2}+3}$),
令y=0解得,x=-$\frac{{k}^{2}}{4{k}^{2}+3}$,
故D(-$\frac{{k}^{2}}{4{k}^{2}+3}$,0),
故|DF1|=|-$\frac{{k}^{2}}{4{k}^{2}+3}$+1|=$\frac{3({k}^{2}+1)}{4{k}^{2}+3}$,
故$\frac{|D{F}_{1}|}{|AB|}$=$\frac{1}{4}$;
综上所述,$\frac{|D{F}_{1}|}{|AB|}$为定值$\frac{1}{4}$.
点评 本题考查了椭圆与直线的位置关系,同时考查了学生的化简运算能力及分类讨论的思想方法应用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=2,φ=-$\frac{π}{6}$ | B. | ω=2,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com