
四个变量 ,
, ,
,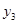 ,
,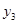 随变量
随变量 变化的数据如下表:
变化的数据如下表:
 | 0 | 5 | 10 | 15 | 20 | 25 |
 | 5 | 130 | 505 | 1130 | 2005 | 3130 |
 | 5 | 94.478 | 1785.2 | 33733 | 6.37 | 1.2 |
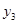 | 5 | 30 | 55 | 80 | 105 | 130 |
 | 5 | 2.3107 | 1.4295 | 1.11407 | 1.0461 | 1.0151 |
 呈指数型函数变化的变量是( )
呈指数型函数变化的变量是( ) B.
B. C.
C.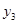 D.
D.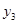
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
工人月工资y(元)与劳动生产率x(千元)变化的回归方程 ,下列判断正确的是 ( )
,下列判断正确的是 ( )
①劳动生产率为1千元时,工资约为130元
②劳动生产率提高1千元时,月工资约提高80元
③劳动生产率提高1千元时,月工资约提高130元
④当月工资为210元时,劳动生产率约为2千元
| A.① ② | B.① ② ④ | C.② ④ | D.① ② ③ ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
甲、乙两人在 次测评中的成绩由右边茎叶图表示(均为整数),其中有一个数字无法看清,现用字母
次测评中的成绩由右边茎叶图表示(均为整数),其中有一个数字无法看清,现用字母 代替,则甲的平均成绩超过乙的平均成绩的概率为( ).
代替,则甲的平均成绩超过乙的平均成绩的概率为( ).
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下 ,其中拟合效果最好的模型是( )
如下 ,其中拟合效果最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 | B.模型2的相关指数 为0.80 为0.80 |
C.模型3的相关指数 为0.50 为0.50 | D.模型4的相关指数 为0.25 为0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设某大学的女生体重 (单位:kg)与身高
(单位:kg)与身高 (单位:cm)具有线性相关关系,根据一组样本数据(
(单位:cm)具有线性相关关系,根据一组样本数据( )(
)( =1,2,…,n),用最小二乘法建立的回归方程为
=1,2,…,n),用最小二乘法建立的回归方程为 =0.85
=0.85 —85.71,则下列结论其中正确的个数是( )
—85.71,则下列结论其中正确的个数是( )
① y与x具有负的线性相关关系
② 回归直线过样本点的中心( ,
, )
)
③ 若该大学某女生身高增加1cm,则其体重约增加0.85kg
④ 若该大学某女生身高为170cm,则可断定其体重必为58.79kg
| A.0 | B.1 | C. 2 | D. 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列对一组数据的分析,不正确的说法是
| A.数据极差越小,样本数据分布越集中、稳定 |
| B.数据平均数越小,样本数据分布越集中、稳定 |
| C.数据标准差越小,样本数据分布越集中、稳定 |
| D.数据方差越小,样本数据分布越集中、稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某学生四次模拟考试时,其英语作文的扣分情况如下表:
考试次数 | 1 | 2 | 3 | 4 |
所减分数 | 4.5 | 4 | 3 | 2.5 |
 与模拟考试次数
与模拟考试次数 之间有较好的线性相关关系,则其线性回归方程为( )
之间有较好的线性相关关系,则其线性回归方程为( ) B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一个容量为20的样本数据分组后,组距与频数如下:(10,20),2;(20,30),3;(30,40),4;(40,50),5;(50,60),4,(60,70),2.则样本在区间(-∞,50)上的频率是( )
| A.0.20 | B.0.25 | C.0.50 | D.0.70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com