
【题目】已知函数![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)设函数![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)见解析.
上单调递增;(2)见解析.
【解析】试题分析:(1)先求函数导数,根据导函数零点情况分类讨论:当![]() 时,仅有一个零点1;当
时,仅有一个零点1;当![]() 时,两个相同的零点;当
时,两个相同的零点;当![]() 及
及![]() 时,两个不同的零点,最后根据导函数符号变化规律确定单调性,(2)先等价转化所证不等式:
时,两个不同的零点,最后根据导函数符号变化规律确定单调性,(2)先等价转化所证不等式: ![]() ①且
①且![]() ②,然后分别利用导数研究函数最值:
②,然后分别利用导数研究函数最值: ![]() 的最小值为
的最小值为![]()
![]() ,
, ![]() 的最小值为
的最小值为![]()
![]()
试题解析:(Ⅰ) ![]()
![]()
![]()
![]()
(1)当![]() 时,
时, ![]() ,当
,当![]() ,
, ![]() ;当
;当![]() ,
, ![]() ;
;
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]() 时,令
时,令![]() ,得
,得![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() 或
或![]() ,
,
所以![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(3)当![]() 时,令
时,令![]() ,
, ![]() ,故
,故![]() 在
在![]() 上递增.
上递增.
(4)当![]() 时,令
时,令![]() ,得
,得![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() 或
或![]() ,
,
所以![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
当![]() 时,
时, ![]() 在
在![]() 上递增.
上递增.
当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)![]()
![]()
![]() ①且
①且![]() ②
②
先证①:令![]() ,则
,则![]() ,
,
当![]() ,
, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
所以![]()
![]()
![]() ,故①成立!
,故①成立!
再证②:由(Ⅰ),当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]()
![]() ,故②成立!
,故②成立!
综上, ![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为![]() +
+![]() =1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
=1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线
,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面ABCD绕着轴
如图所示.将轴截面ABCD绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点P.
相交于点P.
(Ⅰ)求曲线![]() 长度;
长度;
(Ⅱ)当![]() 时,求点
时,求点![]() 到平面APB的距离;
到平面APB的距离;
(Ⅲ)证明:不存在![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若奇函数y=f(x)在区间(0,+∞)上是增函数,又f(﹣3)=0,则不等式f(x)<0的解集为( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(0,3)
D.(﹣∞,﹣3)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
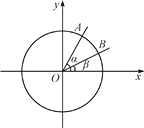
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]() ,
, ![]() .求:
.求:
(1)tan(α+β)的值;
(2)α+2β的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,将
,将![]() 沿
沿![]() 折起,使
折起,使![]() 点到达
点到达![]() 点.
点.
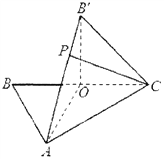
(1)求证: ![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,试问在线段
的体积最大时,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com