
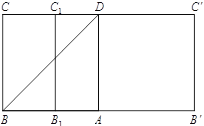
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线
,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面ABCD绕着轴
如图所示.将轴截面ABCD绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点P.
相交于点P.
(Ⅰ)求曲线![]() 长度;
长度;
(Ⅱ)当![]() 时,求点
时,求点![]() 到平面APB的距离;
到平面APB的距离;
(Ⅲ)证明:不存在![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() .
.
【答案】(Ⅰ) ![]() (Ⅱ) 不存在
(Ⅱ) 不存在
【解析】试题分析:(Ⅰ)在侧面展开图中根据几何性质求解;(Ⅱ) 建立如图所示的空间直角坐标系,求出平面ABP的一个法向量及向量![]() ,利用空间向量点到直线距离公式求解;(Ⅲ)假设存在满足要求的
,利用空间向量点到直线距离公式求解;(Ⅲ)假设存在满足要求的![]() ,在空间坐标系中求出法向量,根据空间向量夹角余弦公式,列出关于
,在空间坐标系中求出法向量,根据空间向量夹角余弦公式,列出关于![]() 的方程,看是否有解即可.
的方程,看是否有解即可.
 试题解析:(Ⅰ)
试题解析:(Ⅰ) ![]() 在侧面展开图中为BD的长,其中AB = AD = π,
在侧面展开图中为BD的长,其中AB = AD = π,
∴![]() 的长为
的长为![]() ;
;
(Ⅱ)当![]() 时,建立如图所示的空间直角坐标系,
时,建立如图所示的空间直角坐标系,
则有![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() 、
、![]() 、
、![]()
设平面ABP的法向量为![]() ,则
,则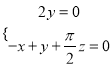 ,
,
取z = 2得![]() ,所以点C1到平面PAB的距离为
,所以点C1到平面PAB的距离为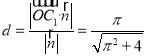 ;
;
注:本题也可以使用等积法求解.
(Ⅲ) 假设存在满足要求的![]() ,
,
 在(II)的坐标系中,
在(II)的坐标系中, ![]() ,
,
![]() ,
,
设平面ABP的法向量为![]() ,则
,则
![]() ,
,
取x1 = 1得![]() ,
,
又平面ABD的法向量为![]() ,
,
由二面角![]() 的大小为
的大小为![]() ,
,
则
![]() .
.
∵![]() ,∴
,∴![]() 时,均有
时,均有![]() ,与上式矛盾.
,与上式矛盾.
所以不存在![]() 使得二面角
使得二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是平行四边行,
是平行四边行, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)证明: ![]() //平面
//平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(4)求二面角![]() 的平面角的正切值.
的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆![]() 上有四个不同的点到直线
上有四个不同的点到直线![]() 的距离为2,则
的距离为2,则![]() 的取值范围是( )
的取值范围是( )
A. (-12,8) B. (-8,12) C. (-13,17) D. (-17,13)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知∠A1,∠A2,…,∠An为凸多边形的内角,且lg sin A1+lg sin A2+…+lg sin An=0,则这个多边形是( )
A. 正六边形 B. 梯形
C. 矩形 D. 含锐角的菱形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
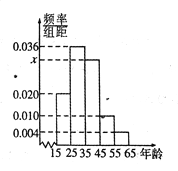
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com