Question

【题目】如图，四棱锥的底面是平行四边形，侧面是边长为2的正三角形， , .

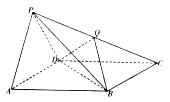
（Ⅰ）求证：平面平面；

（Ⅱ）设是棱上的点，当平面时，求二面角的余弦值.

Answer 1

【答案】（Ⅰ）见解析; （Ⅱ）.

【解析】试题分析：（Ⅰ）要证平面平面，只需证平面即可.

（Ⅱ）分别以、、所在直线为轴、轴、轴建立空间直角坐标系如图，求平面的一个法向量和平面的一个法向量求解即可.

试题解析：

（Ⅰ）取的中点，连接， ，

因为是边长为2的正三角形，所以， ，①

又，所以，且，

于是，从而，②

由①②得平面，而平面，所以平面平面.

（Ⅱ）连结，设，则为的中点，连结，当平面时， ，所以是的中点.

由（Ⅰ）知， 、、两两垂直，分别以、、所在直线为轴、轴、轴建立空间直角坐标系如图，则、、、，

由、坐标得，从而， ，

设是平面的一个法向量，则由得，

取，得，易知平面的一个法向量是，

所以 ，

由图可知，二面角的平面角为钝角，故所求余弦值为.