
设函数
(1)求 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(3)画出函数 在区间
在区间 上的图像(完成列表并作图)。
上的图像(完成列表并作图)。
(1)列表
| x | 0 | |  | |  |  |
| y | | -1 | | 1 | | |

(1)2;(2) ;(3)见解析
;(3)见解析
解析试题分析:(1)由正弦函数周期公式得,
科目:高中数学
来源:
题型:解答题
保持正弦曲线上所有点的纵坐标不变,横坐标缩短为原来的
科目:高中数学
来源:
题型:解答题
(本小题满分12分)定义在区间
科目:高中数学
来源:
题型:解答题
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 =
= ,即可求得
,即可求得 ;(2)将
;(2)将 代入
代入 的解析式,得到关于
的解析式,得到关于 的方程,结合诱导公式即可求出
的方程,结合诱导公式即可求出 ,再利用平方关系结合
,再利用平方关系结合 的范围,求出
的范围,求出 ,再利用商关系求出
,再利用商关系求出 ;(3)先由
;(3)先由 为0和
为0和 算出
算出 分别等于
分别等于 ,
, ,在(
,在( ,
, )分别令
)分别令 取
取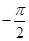 ,0,
,0, ,
, 求出相应的
求出相应的 值和
值和 值,在给定的坐标系中描出
值,在给定的坐标系中描出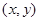 点,再用平滑的曲线连起来,就得到所要作的图像.
点,再用平滑的曲线连起来,就得到所要作的图像.
试题解析:(1)
 ,
, 
 2分
2分
(2)由(1)知
由 得:
得: , 4分
, 4分
∵ ∴
∴ 6分
6分
∴ . 8分
. 8分
(其他写法参照给分)
(3)由(1)知 ,于是有
,于是有
(1)列表x 0 




y 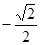
-1 0 1 

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
 ,再将图像沿
,再将图像沿 轴向右平移
轴向右平移 个单位,得到函数
个单位,得到函数 的图像.
的图像.
(1)写出 的表达式,并计算
的表达式,并计算 .
.
(2)求出 在
在 上的值域.
上的值域. 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示.
图象如图所示.
(1)求函数 在
在 的表达式;
的表达式;
(2)求方程 的解;
的解;
(3)是否存在常数 的值,使得
的值,使得 在
在 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. ,
, 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A, 和
和 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设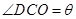 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号