
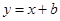 与抛物线
与抛物线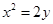 交于A、B两点,O为坐标原点,且
交于A、B两点,O为坐标原点,且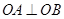 ,则
,则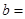 ( )
( )
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:解答题
 时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?
时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
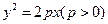 ,过定点
,过定点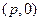 作两条互相垂直的直线
作两条互相垂直的直线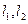 ,若
,若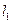 与抛物线交于点
与抛物线交于点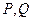 ,
,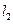 与抛物线交于
与抛物线交于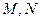 点,
点,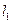 的斜率为
的斜率为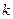 .某同学已正确求得弦
.某同学已正确求得弦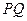 的中点坐标为
的中点坐标为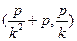 ,请写出弦
,请写出弦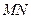 的中点坐标 .
的中点坐标 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
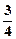 m,则水面上涨到与抛物线拱顶相距
m,则水面上涨到与抛物线拱顶相距查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com