
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题: 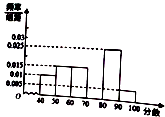
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
【答案】
(1)解:由频率分布直方图得第四小组的频率为:
1﹣(0.01+0.015+0.015+0.025+0.005)×10=0.3.
频率分布直方图如下图.
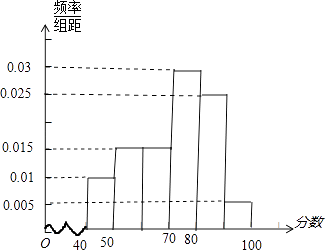
(2)解: 估计这次考试的及格率(60分)及以上为及格)为:
1﹣0.01×10﹣0.015×10=75%,
平均分:45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
【解析】(1)由频率分布直方图中小矩形面积之和为1,能求出第四小组的频率,从而能作出频率分布直方图.(2)由频率分布直方图能估计这次考试的及格率和平均分.
【考点精析】通过灵活运用频率分布直方图和平均数、中位数、众数,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a1=﹣2,公差d=3;数列{bn}中,Sn为其前n项和,满足:2nSn+1=2n(n∈N+)
(Ⅰ)记An= ![]() ,求数列An的前n项和S;
,求数列An的前n项和S;
(Ⅱ)求证:数列{bn}是等比数列;
(Ⅲ)设数列{cn}满足cn=anbn , Tn为数列{cn}的前n项积,若数列{xn}满足x1=c2﹣c1 , 且xn= ![]() ,求数列{xn}的最大值.
,求数列{xn}的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x![]() 时,
时,
恒有f(x)>g(x)成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某商业中心O有通往正东方向和北偏东30方向的两条街道,某公园P位于商业中心北偏东![]() 角(
角(![]() ),且与商业中心O的距离为
),且与商业中心O的距离为![]() 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
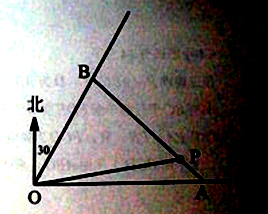
(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法,对于求一个n次多项式函数fn(x)=anxn+an﹣1xn﹣1+…+a1x+a0的具体函数值,运用常规方法计算出结果最多需要n次加法和 ![]() 乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5﹣x4+3x3﹣5x当x=3时的值时,最先计算的是( )
A.﹣5×3=﹣15
B.0.5×3+4=5.5
C.3×33﹣5×3=66
D.0.5×36+4×35=1336.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
:![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(
=( ![]() sinx,sinx),x∈R设函数f(x)=
sinx,sinx),x∈R设函数f(x)= ![]() ﹣
﹣ ![]()
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com